Cho tam giác ABC với điểm M nằm trong tam giác. Các tia AM, BM, CM cắt các cạnh BC, CA, AB tương ứng tại D, E, F. Gọi K là giao điểm của DE và CM. Gọi H là giao điểm của DF và EM. Chứng minh rằng các đường thẳng đồng quy.
Giải bởi qa.haylamdo.com
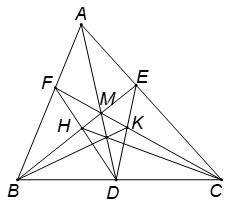
Áp dụng định lí Ménélaus cho tam giác AMC (với bộ ba điểm thẳng hàng E, K, D) và tam giác BMA (với bộ ba điểm thẳng hàng F, H, D), ta có
Suy ra (1)
Áp dụng định lí Céva cho tam giác ABC với bộ ba đường thẳng đồng quy : .
Từ đó: (2)
Từ (1) và (2) ta có: .
Vậy theo phần đảo của định lí Céva, đồng quy, hay đồng quy.
Trong một vườn cây có 9 cây. Hãy trồng thành 10 hàng, mỗi hàng có 3 cây.
Trong một vườn cây có 20 cây. Hãy trồng thành 20 hàng, mỗi hàng có 4 cây.
Trong một vườn cây có 9 cây. Hãy trồng thành 9 hàng, mỗi hàng có 3 cây.
Trong một vườn cây có 20 cây. Hãy trồng thành 18 hàng, mỗi hàng có 4 cây.
Cho hai bộ ba điểm thẳng hàng A, B, C; A', B', C'. Gọi giao điểm của AB' và A'B là A''; AC' và A'C là B''; BC' và B'C là C''. Chứng minh rằng ba điểm A'', B'', C'' thẳng hàng.
Trong một vườn cây có 10 cây. Hãy trồng thành 12 hàng, mỗi hàng có 3 cây.
Trong một vườn cây có 10 cây. Hãy trồng thành 5 hàng, mỗi hàng có 4 cây.
