Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: \[\overrightarrow {K{\rm{A}}} + \overrightarrow {KC} = \overrightarrow 0 \]; \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \]; \[\overrightarrow {HA} + \overrightarrow {H{\rm{D}}} + \overrightarrow {HC} = \overrightarrow 0 \]. Tính độ dài các vectơ \[\overrightarrow {GH} \].
A. \[\frac{{\sqrt 2 a}}{2}\];
B. \[\sqrt 2 \]a;
C. \[\frac{{\sqrt 2 a}}{3}\];
D. a
Giải bởi qa.haylamdo.com
Đáp án đúng là C
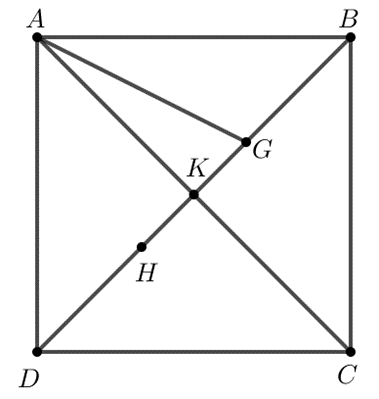
Do \[\overrightarrow {K{\rm{A}}} + \overrightarrow {KC} = \overrightarrow 0 \] nên K là trung điểm của AC.
Do đó K là giao điểm hai đường chéo của hình vuông ABCD.
Do \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \] nên G là trọng tâm của tam giác ABC.
Khi đó trên đoạn BK chọn điểm G sao cho \[\overrightarrow {BG} = \frac{2}{3}\overrightarrow {BK} \].
Do \[\overrightarrow {HA} + \overrightarrow {H{\rm{D}}} + \overrightarrow {HC} = \overrightarrow 0 \] nên H là trọng tâm của tam giác ADC.
Khi đó trên đoạn DK chọn điểm H sao cho \[\overrightarrow {DH} = \frac{2}{3}\overrightarrow {DK} \].
Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:
AC2 = AD2 + DC2
\[ \Rightarrow \] AC2 = a2 + a2
\[ \Rightarrow \] AC2 = 2a2
\[ \Rightarrow \] AC = \[\sqrt 2 \]a (do AC là độ dài đoạn thẳng nên AC > 0)
Do K là trung điểm của AC nên AK = \[\frac{1}{2}\]AC = \[\frac{{\sqrt 2 a}}{2}\].
Do đó \[\left| {\overrightarrow {K{\rm{A}}} } \right| = \frac{{\sqrt 2 a}}{2}\].
Do ABCD là hình vuông nên AC = BD.
Do đó BD = \[\sqrt 2 \]a.
Do H là trọng tâm của tam giác ADC nên HK = \[\frac{1}{3}\]DK = \[\frac{1}{3}.\frac{1}{2}\]BD = \[\frac{1}{6}\]BD = \[\frac{{\sqrt 2 a}}{6}\].
Do G là trọng tâm của tam giác ABC nên KG = \[\frac{1}{3}\]BK = \[\frac{1}{3}.\frac{1}{2}\]BD = \[\frac{1}{6}\]BD = \[\frac{{\sqrt 2 a}}{6}\].
Do đó HK + KG = \[\frac{{\sqrt 2 a}}{6}\]+ \[\frac{{\sqrt 2 a}}{6}\] hay HG = \[\frac{{\sqrt 2 a}}{3}\].
Do đó \[\left| {\overrightarrow {GH} } \right| = \frac{{\sqrt 2 a}}{3}\].
Cho tam giác ABC có I là trung điểm cạnh AB và G là trọng tâm tam giác ABC. Đẳng thức nào sau đây sai:
Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \).
Cho hình bình hành ABCD có một điểm O bất kì. Đẳng thức nào sau đây đúng?
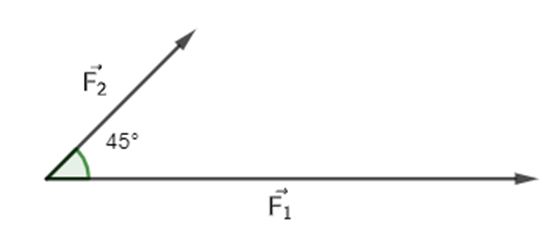
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 7N,\left| {\overrightarrow {{F_2}} } \right| = 3N\). Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)(biết góc giữa \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) bằng 45°).
Cho hình vuông ABCD có cạnh bằng 1. So sánh độ dài của hai vectơ sau:
\[\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {B{\rm{D}}} } \right) + \overrightarrow {CB} \];
\[\overrightarrow b = \overrightarrow {AB} + \overrightarrow {A{\rm{D}}} + \overrightarrow {BC} + \overrightarrow {DA} \].
Cho hình bình hành ABCD có tâm O, G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
Tính tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \)
Cho lục giác đều ABCDEF và O là tâm. Có bao nhiêu đẳng thức dưới đây là đẳng thức đúng?
1. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow 0 \);
II. \(\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AD} \);
III. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow {EB} \);
IV. \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FE} = \overrightarrow 0 \).
Cho hình thoi ABCD có độ dài cạnh bằng 2 dm và \(\widehat {BAD} = 100^\circ \). Tính độ dài vectơ \(\overrightarrow {DA} + \overrightarrow {DC} \).
Cho hình bình hành ABCD. Hãy tìm điểm M để \(\overrightarrow {DM} = \overrightarrow {CB} + \overrightarrow {CD} \).
Cho hình bình hành ABCD tâm O. Ba điểm M, N, P thỏa mãn:
+) \[\overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {MB} = \overrightarrow 0 \];
+) \[\overrightarrow {N{\rm{D}}} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \];
+) \[\overrightarrow {PM} + \overrightarrow {PN} = \overrightarrow 0 \].
Nhận xét nào sau đây đúng về M, N, P.
Hai người cùng kéo một con thuyền với hai lực \[\overrightarrow {{F_1}} = \overrightarrow {OA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {OB} \] có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.
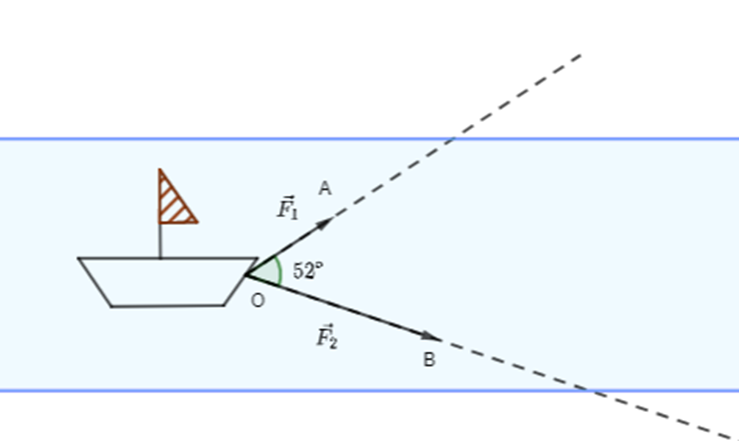
Độ lớn của vectơ hợp lực \[\overrightarrow F \] là tổng của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] nằm trong khoảng nào dưới đây?
