Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a, b, c.
A. \[\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\];
B. \[\frac{{{b^2} + {c^2} - {a^2}}}{4}\];
C. \[{b^2} + {c^2} - {a^2}\];
D. \(\frac{{{b^2} + {c^2} - {a^2}}}{2}\)
Giải bởi qa.haylamdo.com
Đáp án đúng là D
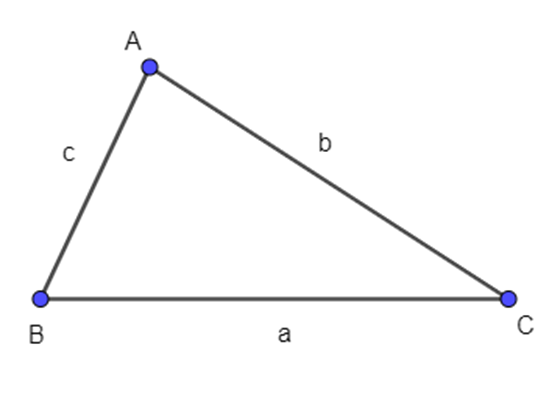
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right) = AB.AC.\cos BAC = bc.c{\rm{osBAC}}\)
Theo định lí cos, ta có:
\[{\rm{cosBAC = }}\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\]
\(\overrightarrow {AB} .\overrightarrow {AC} = bc.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\).
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}.\)
Khi nào thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc?
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; -3), B(5; 2). Tìm điểm M thuộc tia Oy để góc \(\widehat {AMB} = {90^0}.\)
Cho tam giác ABC có trọng tâm G. Với điểm M bất kì, đẳng thức nào sau đây đúng?
Tính tích vô hướng của hai vectơ \(\overrightarrow u \left( {1; - 3} \right),\overrightarrow v \left( {\sqrt 7 ;\,\, - 2} \right)\) là k. Nhận xét nào sau đây đúng về giá trị của k.
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
Cho tam giác ABC với A(-1;2), B(8;-1), C(8;8). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
Góc giữa vectơ \(\overrightarrow a \left( { - 1; - 1} \right)\) và vecto \(\overrightarrow b \left( { - 1;0} \right)\) có số đo bằng:
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(-3;1), B(2;4), C(2;-2). Gọi H(x; y) là trực tâm của tam giác ABC. Tính S = 5x + y.
Tìm điều kiện của \(\overrightarrow u ,\overrightarrow v \) để \(\overrightarrow u .\overrightarrow v = - \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\)
Khi nào thì \({\left( {\overrightarrow u .\overrightarrow v } \right)^2} = {\overrightarrow u ^2}.{\overrightarrow v ^2}?\)
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) trong trường hợp \(\overrightarrow a \left( {3;1} \right),\overrightarrow b \left( {2;4} \right)\).
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
