Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
A. \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^0}.\)
B. \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^0}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = {a^2}.\)
C. \(\overrightarrow {AC} .\overrightarrow {BD} = {a^2}\sqrt 2 .\)
D. \(\overrightarrow {BA} .\overrightarrow {BD} = - {a^2}.\)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là B
Vì ABCD là hình vuông cạnh a nên AB = BC = a, BD = AC = a\(\sqrt 2 \).
Ta có \(\overrightarrow {AB} \left( {a;\,\,0} \right)\), \(\overrightarrow {BD} \left( { - a;\,\,a} \right)\), \(\overrightarrow {AC} \left( {a;\,\,a} \right)\), \(\overrightarrow {BC} \left( {0;\,\,a} \right)\), \(\overrightarrow {BA} \left( { - a;\,\,0} \right)\).
Khi đó:
+) \(\overrightarrow {AB} .\overrightarrow {BD} = a.\left( { - a} \right) + 0.a = - {a^2}\)
\( \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {BD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|}} = \frac{{ - {a^2}}}{{a.a\sqrt 2 }} = \frac{{ - 1}}{{\sqrt 2 }} \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {135^0}.\) Do đó A sai.
+) \(\overrightarrow {AC} .\overrightarrow {BC} \) = a.0 + a.a = a2
\( \Rightarrow \cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {BC} }}{{\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{{a^2}}}{{a.a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^0}.\) Do đó B đúng
+) \(\overrightarrow {AC} .\overrightarrow {BD} = a.\left( { - a} \right) + a.a = 0\). Do đó C sai.
+) \(\overrightarrow {BA} .\overrightarrow {BD} \) = -a.(-a) + 0.a = a2. Do đó D sai.
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
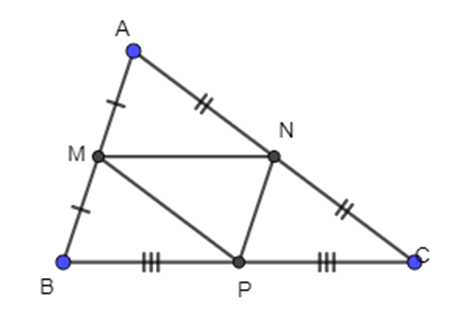
Phát biểu nào dưới đây là sai.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
Khi nào thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc?
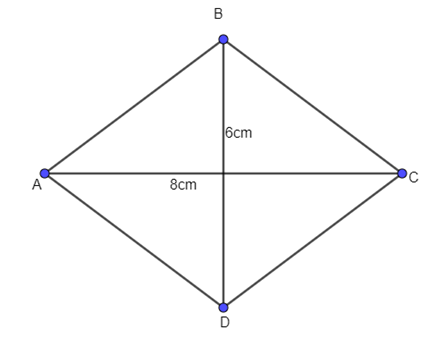
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Cho hình vẽ:
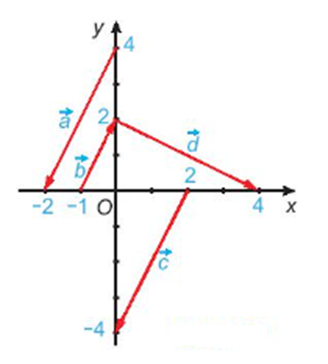
Có bao nhiêu cặp vectơ không cùng phương trên hình vẽ?
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 5\overrightarrow i + 6\overrightarrow j .\) Khi đó tọa độ của vectơ \(\overrightarrow u \)là: