Cho hình chữ nhật ABCD có AB = 4, BC = 6. M là trung điểm của BC, N là điểm trên cạnh CD sao cho ND = 3NC. Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng:
A.
B.
C.
D.
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: D
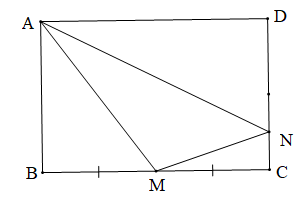
Vì M là trung điểm của BC nên BM = MC = 3.
Vì ND = 3NC nên NC = 1 và ND = 3.
Tam giác CMN vuông tại C theo định lí Py – ta – go có:
MN2 = MC2 + NC2 = 32 + 12 = 10
Tam giác AND vuông tại D theo định lí Py – ta – go có:
AN2 = AD2 + DN2 = 62 + 32 = 45
Tam giác ABM vuông tại B theo định lí Py – ta – go ta có:
AM2 = AB2 + BM2 = 42 + 32 = 25 Þ AM = 5.
Nửa chu vi của tam giác AMN là:
Diện tích tam giác AMN theo công thức Heron là:
(đơn vị diện tích)
Mặt khác
Vậy bán kính đường tròn ngoại tiếp tam giác AMN bằng
Tam giác ABC có . Gọi D là chân đường phân giác trong góc A. Khi đó số đo của góc ADB là:
Một tam giác có ba cạnh là 52, 56, 60. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó R. r bằng:
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng . Số đo góc A là:
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
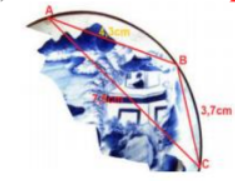
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Tam giác ABC có với BC = a, AC = b, AB = c thì câu nào sau đây là đúng?
Cho tam giác ABC có AB = 8, AC = 9, BC = 10. Tam giác ABC là tam giác:
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
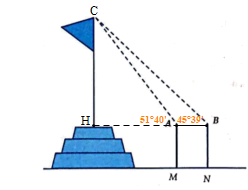
Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:
