 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hàm số f(x) = 4x + 5
Chọn x1, x2 tùy ý thuộc (–∞; 2) sao cho x1 > x2 ta có: f(x1) – f(x2) = (4x1 + 5) – (4x2 + 5) = 4x1 – 4x2 = 4(x1 – x2)
Ta có: x1 > x2 ⇒ x1 – x2 > 0 ⇒ f(x1) – f(x2) > 0 ⇒ f(x1) > f(x2)
Do đó, hàm số f(x) = 4x + 5 đồng biến trên khoảng (–∞; 2).
Chọn x1, x2 tùy ý thuộc (2; +∞) sao cho x1 > x2 ta có: f(x1) – f(x2) = (4x1 + 5) – (4x2 + 5) = 4x1 – 4x2 = 4(x1 – x2)
Ta có: x1 > x2 ⇒ x1 – x2 > 0 ⇒ f(x1) – f(x2) > 0 ⇒ f(x1) > f(x2)
Do đó, hàm số f(x) = 4x + 5 đồng biến trên khoảng (2; +∞).
Cho hàm số có đồ thị như hình dưới:
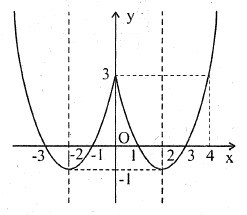
Khẳng định nào dưới đây là đúng ?
Cho hàm số có đồ thị như hình dưới:
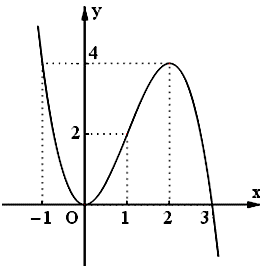
Khẳng định nào dưới đây là sai ?
Cho hàm số có đồ thị như hình dưới:
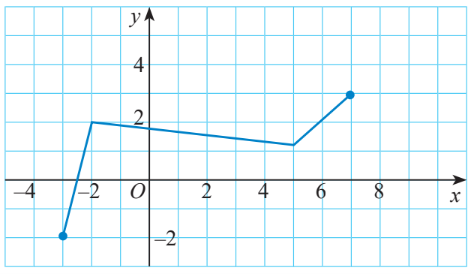
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng (–3; –2), (–2; 5), (5; 7).
Cho hàm số có đồ thị như hình dưới:
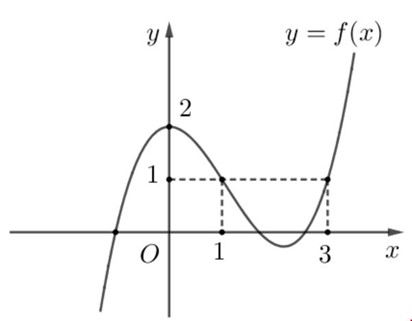
Khẳng định nào dưới đây là đúng ?