Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC. Vectơ nào sau đây bằng vectơ .
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải:
Đáp án đúng là: B.
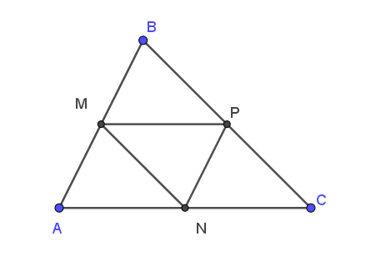
Xét tam giác ABC có:
N là trung điểm của AC có: NC = AC (1)
M là trung điểm của AB, P là trung điểm của BC nên MP là đường trung bình của tam giác ABC, do đó: MP = AC (2), MP // AC (3)
Từ (1) và (2) ta suy ra: NC = MP hay .
Từ (3) ta có: hai vectơ và cùng phương, mà chúng cùng hướng đi từ trái sang phải.
Vậy = .
Cho hình vuông ABCD tâm O như hình vẽ sau:
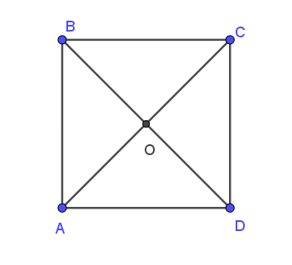
Vectơ nào sau đây bằng vectơ ?
Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ.
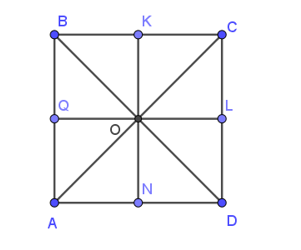
Khẳng định nào sau đây là đúng ?
Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC. Vectơ nào là vectơ đối của vectơ ?
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC. Vectơ nào sau đây là vectơ đối của .
Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC như hình vẽ.
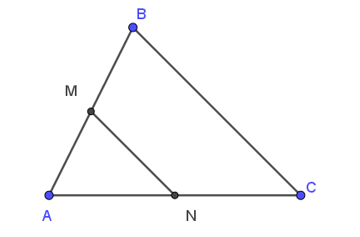
Vectơ nào bằng vectơ ?
Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ.
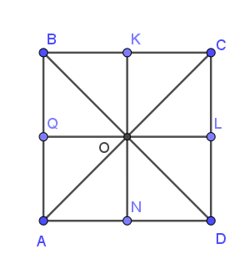
Khẳng định nào sau đây là sai ?
Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của các cạnh AB, AD, CD, CB.
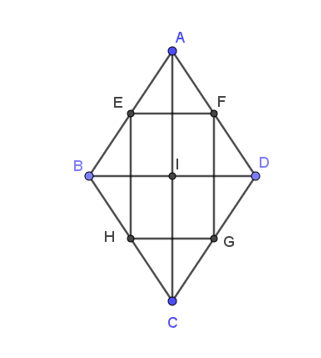
Khẳng định nào sau đây là đúng ?
Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của các cạnh AB, AD, CD, CB và J, L, K, M lần lượt là giao điểm của HE với BD, EF với AC, FG với BD, GH với AC.
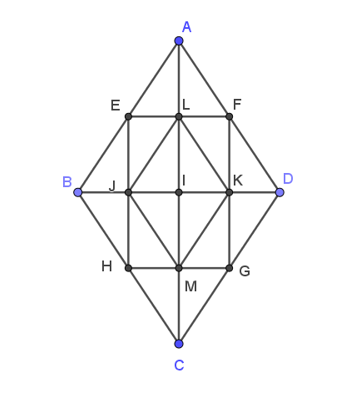
Khẳng định nào sau đây là sai ?