Tam giác DEF có số đo như hình vẽ dưới đây.
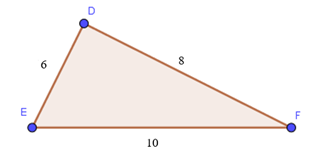
Số đo của góc DEF gần nhất với giá trị:
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có: DE2 + DF2 = 62 + 82 = 100; EF2 = 102 = 100.
Suy ra DE2 + DF2 = EF2.
Do đó tam giác DEF vuông tại D (theo định lí Pythagore đảo).
Khi đó ta có: cosDEF = \(\frac{{DE}}{{EF}} = \frac{6}{{10}} = \frac{3}{5}\).
Ấn máy tính, ta tính được \[\widehat {DEF} \approx 53^\circ \].
Cho α = 23°56'. Giá trị của cot α gần nhất với giá trị nào sau đây?
Tìm tất cả giá trị của α (0° ≤ α ≤ 180°) thỏa mãn sin α = \(\frac{4}{{11}}\).
Cho α (0° ≤ α ≤ 180°) thỏa mãn cot α = 7,486. Giá trị của α gần nhất với: