Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: B
Trường hợp 1: x ≤ 0.
Biểu thức f(x) = \(\frac{{ - 1}}{{x - 1}}\) xác định khi và chỉ khi x – 1 ≠ 0.
Nghĩa là, x ≠ 1.
Giao với điều kiện x ≤ 0, ta được x ≤ 0.
Trường hợp 2: x > 0.
Biểu thức f(x) = \(\sqrt {x + 2} \) xác định khi và chỉ khi x + 2 ≥ 0.
Nghĩa là, x ≥ –2.
Giao với điều kiện x > 0, ta được x > 0.
Vì vậy khi hợp điều kiện của trường hợp 1 và trường hợp 2, ta thu được tập xác định của hàm số là D = ℝ.
Vậy ta chọn phương án B.
Hàm số y = f(x) có đồ thị như hình vẽ bên.
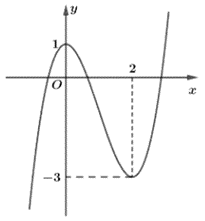
Khẳng định nào sau đây đúng?
Điểm nào sau đây thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\]?
Xét tính đồng biến, nghịch biến của hàm số \(y = \sqrt[3]{x} + 3\).
