A. 20;
C. 38;
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: D
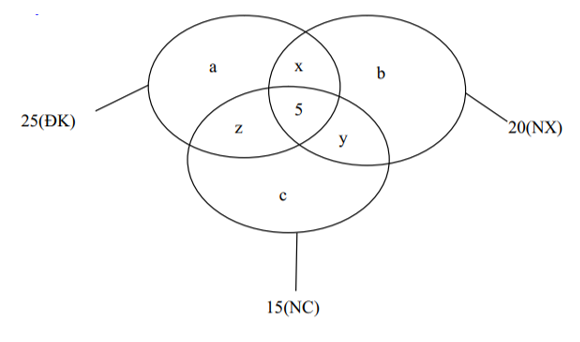
Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
x là số học sinh chỉ thi hai môn điền kinh và nhảy xa.
y là số học sinh chỉ thi hai môn nhảy xa và nhảy cao.
z là số học sinh chỉ thi hai môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là: 45 – 7 = 38
Dựa vào biểu đồ ven ta có hệ phương trình sau:
Cộng vế với vế của (1), (2), (3) ta có: a + b + c + 2(x + y + z) + 15 = 60 (5)
Từ (4) và (5) ta có: a + b + c + 2(38 – 5 – a – b – c) + 15 = 60
⟺ a + b + c = 21.
Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.
Cho mệnh đề chứa biến P(x) = {x ∈ ℤ : |x2 – 2x – 3| = x2 + |2x + 3|}. Trong đoạn [-2020; 2021] có bao nhiêu giá trị của x để mệnh đề chứa biến P(x) là mệnh đề đúng?
Cho A = {x ∈ ℝ | |x – m| ≤ 25}; B = {x ∈ ℝ | |x| ≥ 2020}.
Có bao nhiêu giá trị nguyên m thỏa mãn A ∩ B = ∅.
Cho hai tập hợp P = [3m – 6; 4] và Q = (-2; m + 1), m ∈ ℝ. Tìm m để
P\Q = ∅.