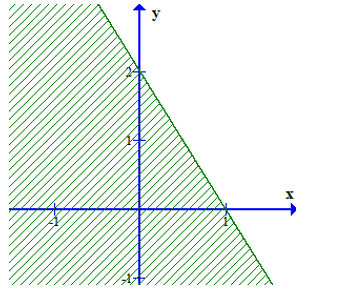
Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình ax + by > c. Tính giá trị của biểu thức P = a2 + b2 – 2c ?
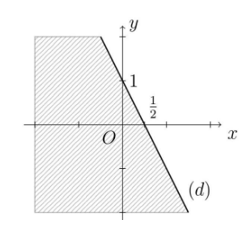
A. P = 3;
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: A
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là và (0; 1). Ta có hệ phương trình
y = – 2x + 1
Vậy đường thẳng có phương trình 2x + y = 1.
Xét điểm O(0; 0), có: 2.0 + 0 = 0 < 1.
Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + y > 1
Suy ra: a = 2; b = 1; c = 1
⇒ P = a2 + b2 – 2c = 22 + 12 – 2.1 = 3.
Vậy P = 3.
Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình ax + by ≥ c. Kết luận nào sau đây đúng?
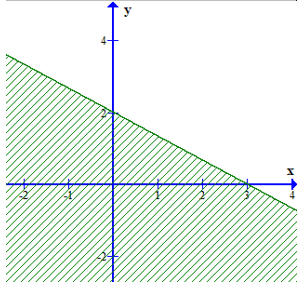
Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình (a – 1)x + (2b + 3)y > – 2. Giá trị của a, b là?
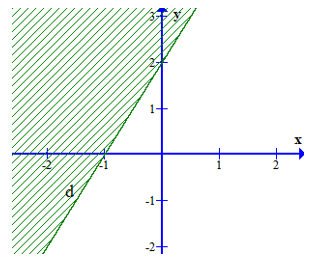
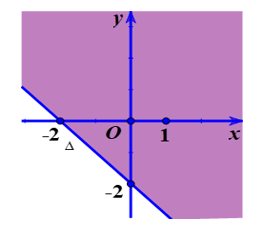
Phần nửa mặt phẳng tô đậm (không kể đường thẳng ∆) trong hình vẽ dưới đây biểu diễn miền nghiệm của bất phương trình ax + by > c. Hệ số a, c là nghiệm của hệ phương trình?
Có bao nhiêu giá trị của m để phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình (m2 – 3m + 2)x – y < – 2.