Từ các chữ số 1; 2; 3; 4; 5; 6, có thể lập được bao nhiêu số tự nhiên bé hơn 100?
A. 36;
B. 62;
C. 54;
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: D
Các số bé hơn 100 là các số có một chữ số và các số có hai chữ số.
Việc lập các số bé hơn 100 từ các chữ số 1; 2; 3; 4; 5; 6 có hai phương án thực hiện:
Phương án 1: Lập số có một chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Khi đó có thể lập được 6 số.
Phương án 2: Lập số có hai chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Gọi là số cần tìm.
Chọn số ở vị trí a, có 6 cách chọn.
Chọn số ở vị trí b, có 6 cách chọn.
Theo quy tắc nhân, ta có 6.6 = 36 cách lập một số có hai chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Vậy theo quy tắc cộng, ta có tất cả 6 + 36 = 42 số tự nhiên bé hơn 100.
Do đó ta chọn phương án D.
Biển số xe máy của tỉnh A (không gồm kí hiệu địa phương đăng kí xe và seri đăng kí) thì có 5 kí tự, mỗi kí tự là một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} và không có biển số xe 000.01. Hỏi nếu hai kí tự đầu tiên đều không nhỏ hơn 7 thì tỉnh A có thể làm được nhiều nhất bao nhiêu biển số xe máy?
Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...
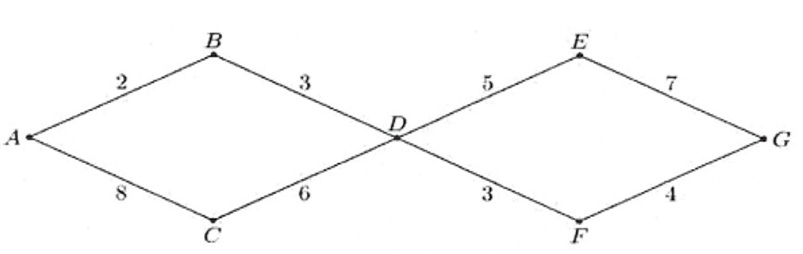
Số con đường từ A đến G là:
Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên có chữ số 1?