Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD và điểm O tùy ý trên mặt phẳng (BCD). Thể tích tứ diện OMNP bằng
A. a3√296.
B. a3√224.
C. a3√248.
D. a3√236.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: D
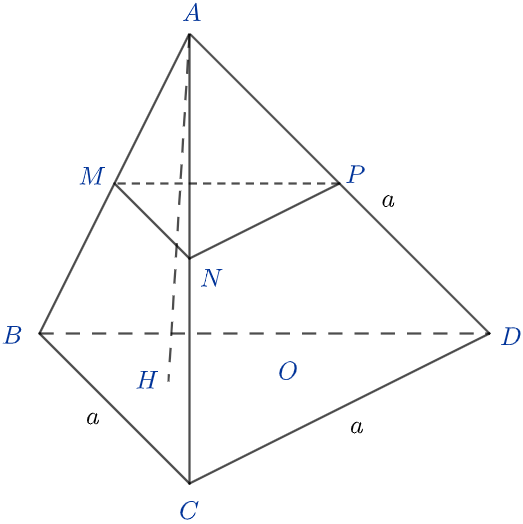
AH là đường cao của tứ diện đều A.BCD nên H là trọng tâm tam giác BCD
Suy ra, HD=a√33
⇒AH=√AD2−HD2
=√a2−(a√33)2=a√63
Và SBCD=12BC.BD.sin^CBD=a2√34
Ta có: AMAB=ANAC=APAD=12
Suy ra mặt phẳng (MNP) song song với mặt phẳng (BCD)
⇒ dO/(MNP) = dB/(MNP) = dA/(MNP)
=12dA/(BCD)=AH2=a√66
SMNP=(AMAB)2.SBCD=14SBCD=a2√316
Suy ra VO.MNP=13dO/(MNP).SMNP
=13.a√66.a2√316=a3√236
Trong mặt phẳng tọa độ Oxy, gọi (C) là đồ thị của hàm số y=x−1x−2. Phương trình tiếp tuyến của (C) tại giao điểm của đồ thị (C) với trục hoành là
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số y=|x|3−6x2+9|x|−3 với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
Tất cả các giá trị của tham số m để hàm số y=x+1x+m đồng biến trên khoảng (-∞; -2) là
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin3 x + 9cos2 x + 6sin x -10. Giá trị của tích M.m bằng
Trong không gian tọa độ Oxyz, gọi (P) là mặt phẳng đi qua 2 điểm A(0; 1; -2), B(2; 1; 0) sao cho khoảng cách từ gốc tọa độ O đến (P) lớn nhất. Phương trình của mặt phẳng (P) là
Cho hàm số f (x) liên tục và có đạo hàm trên [0; 1]. Biết và f (0) = f (1) = 7. Giá trị của tích phân bằng
Gọi F (x) là một nguyên hàm của hàm số f (x) = ex thỏa mãn F (0) = 2. Giá trị của F (1) bằng