Cho số phức z thỏa điều kiện .
Giá trị nhỏ nhất của biểu thức được viết dưới dạng với a, b là các hữu tỉ.
Giá trị của a + b là
A. 4
B. 2
C. 7
D. 3
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án D
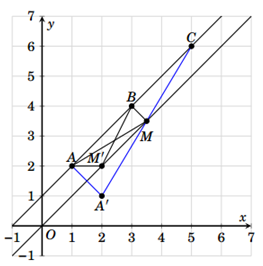
Cách 1
· Đặt ![]() biểu diễn cho số phức z.
biểu diễn cho số phức z.
· Từ giả thiết, ta có M thuộc đường trung trực ![]() của đoạn EF và P=AM+BM+CM
của đoạn EF và P=AM+BM+CM
· Ta chứng minh điểm M chính là hình chiếu vuông góc của B lên đường thẳng .
- Với M’ tùy ý thuộc, M’ khác M. Gọi A’ là điểm đối xứng của A qua . Nhận thấy rằng ba điểm A’, M, C thẳng hàng.
- Ta có ![]()
Mà ![]()
Lại có ![]() Do đó
Do đó ![]()
Cách 2
· Gọi ![]() Từ giả thiết
Từ giả thiết ![]() , dẫn đến y=x .
, dẫn đến y=x .
Khi đó z=x+xi.
· ![]()
· Sử dụng bất đẳng thức ![]()
Dấu đẳng thức xảy ra khi và chỉ khi  . Ta có
. Ta có
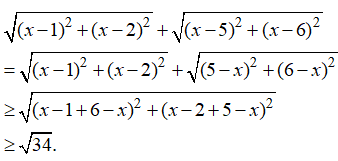
Dấu đẳng thức xảy ra khi và chỉ khi ![]()
· Mặt khác

Dấu đẳng thức xảy ra khi và chỉ khi x=
· Từ hai trường hợp trên, ta thấy, giá trị nhỏ nhất của P là 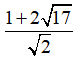 .
.
Khi đó a+b=3.
Cho các số phức z, w thỏa mãn
Tìm giá trị lớn nhất của biểu thức
Cho w là số phức thay đổi thỏa mãn .
Trong mặt phẳng phức, các điểm biểu diễn số phức z=3w+1-2i chạy trên đường nào?
Cho các số phức w,z thỏa mãn và 5w=(2+i)(z-4).
Giá trị lớn nhất của biểu thức bằng
Cho số phức z thỏa mãn . Biết tập hợp các điểm biểu diễn số phức w xác định bởi là một đường tròn bán kính R. Tính R
Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: và ?
Tập hợp tất cả các điểm biễu diễn các số phức z thõa mãn là đường tròn có tâm I và bán kính R lần lượt là
Cho số phức z=1+i. Biết rằng tồn tại các số phức
(trong đó ) thỏa mãn .
Tính b-a.
Cho số phức z, biết rằng các điểm biễu diễn hình học của các số phức z, iz và z+iz tạo thành một tam giác có diện tích bằng 18. Modun của số phức bằng
Gọi là bốn nghiệm phân biệt của phương trình trên tập số phức.
Tính giá trị của biểu thức