Cho các số phức z và w thỏa mãn (3-i)|z|=zw-1+1-i. Tìm GTLN của T=|w+i|.
A. √22.
B. 3√22.
C. 2.
D. 12.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án cần chọn là: B.
Dễ dàng kiểm tra z = 0 không thỏa mãn (3-i)|z|=zw-1+1-i.
Ta có: (3-i)|z|=zw-1+1-i
⇔zw-1=(3-i)|z|+i-1⇔zw-1=(3|z|-1)+(1-|z|)i⇒|zw-1|=√10|z|2-8|z|+2⇒|w-1|=√|z|210|z|2-8|z|+2
Nhận xét:
⇔{|z|=12w-1=12(1+i)z=1+i2.2k1-i⇔{z=i2w=32+12i
Vậy MaxT=3√22.
Cho số phức z có tích phần thực và phần ảo bằng 625. Gọi a là phần thực của số phức z3+4i. Giá trị nhỏ nhất của |a| bằng.
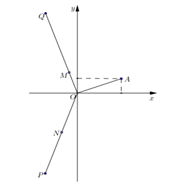
Cho số phức z thỏa mãn |z|=√22 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w=1iz là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
Cho các số phức z thỏa mãn . Biết rằng tập hợp các điểm biểu diễn số phức w=(3-4i)z+i là một đường tròn. Tính bán kính r của đường tròn đó.
Cho số phức z thay đổi, luôn có |z|=2. Khi đó tập hợp điểm biểu diễn số phức w=(1-2i)ˉz+3i là:
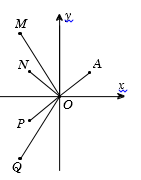
Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
Cho hai số phức khác 0 thỏa mãn là số thuần ảo và . Giá trị lớn nhất của bằng: