Cho hàm số y = x3 + x2 + x + 1. Viết PTT tại M thuộc đồ thị hàm số biết tung độ điểm M bằng 1.
A: y = 2x + 1
B: y = x + 1
C: y = x + 2
D: y = x - 1
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn B.
Đặt f(x) = x3 + x2 + x + 1 ⇒ f’(x) = (x3 + x2 + x + 1)’ = 3x2 + 2x + 1
Gọi M(xM; yM) là tiếp điểm
Theo gt:
Gọi k là hệ số góc của tiếp tuyến tại M; k = f’(0) = 3.0+ 2.0+ 1 = 1
⇒ Pttt tại M có tung độ bằng 1 là: y = 1. (x – 0) + 1
Hay y = x + 1.
Cho hàm số y = -x3 + 3x2 – 2 có đồ thị (C). Số tiếp tuyến của (C) song song với đường thẳng y = -9x là:
Cho hàm số y = x3 – 2x2 + 2x có đồ thị (C). Gọi x1, x2 là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017. Khi đó x1 + x2 bằng:
Tiếp tuyến của đồ thị hàm số 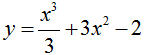 có hệ số góc k = -9 có phương trình là:
có hệ số góc k = -9 có phương trình là:
Phương trình tiếp tuyến của đồ thị hàm số y = x4 + 2x2 – 1 tại điểm có tung độ tiếp điểm bằng 2 là:
Cho hàm số y = x2 – 6x + 5 có tiếp tuyến song song với trục hoành. Phương trình tiếp tuyến đó là:
Phương trình tiếp tuyến của đồ thị hàm số f(x) = x3 – 2x2 + 3x tại điểm có hoành độ xo = -1 là:
Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x3 – 3x2 + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng
Cho hàm số 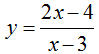 có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:
có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:
Lập phương trình tiếp tuyến của đường cong (C): y = x3 + 3x2 – 8x + 1, biết tiếp tuyến đó song song với đường thẳng Δ: y = x + 2017?
Cho hàm số y = (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây?
Cho hàm số 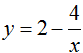 có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
Tìm số f(x) = x3 – 3x2 + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi.
Cho hàm số 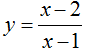 . Viết PTTT của đồ thị hàm số biết . Tiếp điểm M có tung độ bằng 4
. Viết PTTT của đồ thị hàm số biết . Tiếp điểm M có tung độ bằng 4
Cho hàm số ![]() . Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?
. Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?