Giá trị của m để bất phương trình x + 3 < mx + 4 có nghiệm là:
A. ∀x ∈ R
B. m = 0
C. m = 0 và m = 1
D. m = 1
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn A.
x + 3 < mx + 4 ⇔ m(m - 1)x < 1 vô nghiệm 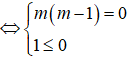
Vậy với ∀m ∈ R, bất phương trình có nghiệm.
Tìm tất cả các giá trị thực của tham số m để f(x) = m(x - m) - (x - 1) không âm với mọi x ∈ (-; m + 1].
Giá trị nào của m thì bất phương trình ( + m + 1)x - 5m ≥ ( + 2)x - 3m - 1 vô nghiệm là:
Cho biểu thức f(x) = (x + 5)(3 - x). Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là