Cho tam giác ABC biết A(-1;2), B(2;-4), C(1;0)
a) Tìm tọa độ trực tâm H của tam giác ABC
b) Viết phương trình đường tròn ngoại tiếp tam giác ABC
c) Viết phương trình tiếp tuyến của đường tròn tại A
Giải bởi qa.haylamdo.com
Cách 1:
Gọi H là trực tâm của tam giác ABC
A(-1;2), B(2;-4), C(1;0) 
Đường thẳng CH là đường thẳng đi qua C nhận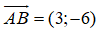 
là vecto pháp tuyến:
CH: 3(x - 1) - 6(y - 0) = 0 ⇔ x - 2y - 1 = 0
Đường thẳng BH là đường thẳng đi qua B nhận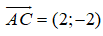 
là vecto pháp tuyến:
BH: 2(x - 2) - 2(y + 4) = 0 ⇔ x - y - 6 = 0
H là giao điểm của CH và BH. Do đó, tọa độ của H là nghiệm của hệ phương trình:
Cách 2:
Gọi H(a;b) là trực tâm của tam giác ABC
Vì H là trực tâm của tam giác ABC nên:
Viết phương trình đường tròn ngoại tiếp tam giác ABC
Gọi phương trình đường tròn ngoại tiếp tam giác ABC có dạng:
(C): + - 2ax - 2by + c = 0(1)
Vì (C) ngoại tiếp tam giác ABC nên tọa độ ba điểm A, B, C thỏa mãn phương trình đường tròn. Ta có hệ phương trình:
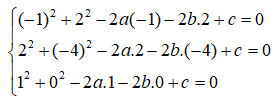
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là:
Viết phương trình tiếp tuyến của đường tròn tại A
Phương trình đường tròn (C) có tâm
Phương trình tiếp tuyến của đường tròn tại A là đường thẳng đi qua A và nhận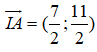 
là vecto pháp tuyến:
Cho elip (E): 4 + 9 = 36. Trong các khẳng định sau, khẳng định nào đúng?
Cho elip (E): + 9 = 9
a) Tìm tọa độ hai tiêu điểm của elip
b) Tìm trên (E) điểm M sao cho MF1 = 2MF2
Đường thẳng qua M(-2;3) và vuông góc với đường thẳng d: 2x - y + 3 = 0 là:
Cho đường thẳng . Phương trình tổng quát của d là:
