Xét tính đồng biến và nghịch biến của hàm số trên các khoảng và .
A. đồng biến trên khoảng và nghịch biến trên khoảng
B. đồng biến trên cả hai khoảng và
C. nghịch biến trên khoảng và đồng biến trên khoảng
D. nghịch biến trên cả hai khoảng và
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Với ta có:
.
· Với thì x1 < 2; x2 <2 nên nên f(x) đồng biến trên khoảng .
· · Với thì x1>2; x2 >2 nên nên f(x) nghịch biến trên khoảng .
Vậy đáp án là A.
Nhận xét: Với 4 phương án trả lời cho ta biết f(x) đồng biến hoặc nghịch biến trên mỗi khoảng và .
Vì vậy, ta lấy hai giá trị bất kì thuộc mỗi khoảng rồi so sánh và . Chẳng hạn có ; nên , suy ra f(x) đồng biến trên khoảng .
Cho hàm số có đồ thị như hình vẽ bên.
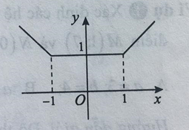
Khẳng định nào sau đây là đúng?
Trong các điểm M( -1; 5); N(1; 4); P(2; 0); Q(3; 1), điểm nào thuộc đồ thị hàm số