18 câu hỏi trắc nghiệm thuộc Hàm số

Câu 1:

Công thức nào sau đây không phải là hàm số?

A. y = x - 1

B. $y = \sqrt{x^{2} + 1}$

C. $y = \frac{1}{x}$

D. $|y| = 5 x$

Công thức $|y| = 5 x$ , ứng với x > 0 tìm được hai giá trị của y là y = 5x và y = -5x nên $|y| = 5 x$ không phải là hàm số.

Vậy đáp án đúng là D.

Câu 2:

Tập xác định của hàm số $y = \sqrt{x - 2} + \frac{1}{\sqrt{x + 2}}$ là:

A. $[- 2; + \infty)$

B. $(- 2; + \infty)$

C. $(2; + \infty)$

D. $[2; + \infty)$

Xem đáp án

Nhận thấy $y = \sqrt{x - 2} + \frac{1}{\sqrt{x + 2}}$ có nghĩa khi $\{\begin{cases} x - 2 \geq 0 \\ x + 2 > 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq 2 \\ x > - 2 \end{cases} \Leftrightarrow x \geq 2$ .

Do đó tập xác định của hàm số đã cho là $[2; + \infty)$ .

Vậy đáp án là D.

Câu 3:

Cho hàm số $y = f (x) = \sqrt{x^{2} - 2 x \sqrt{5} + 5}$ . Tính $f (\sqrt{5} - \sqrt{3})$ .

A. $2 \sqrt{5} - \sqrt{3}$

B. $- 2 \sqrt{5} + \sqrt{3}$

C. $\sqrt{3}$

D. $- \sqrt{3}$

Xem đáp án

Ta có $y = f (x) = \sqrt{{(x - \sqrt{5})}^{2}} = |x - \sqrt{5}|$ nên

$f (\sqrt{5} - \sqrt{3}) = |\sqrt{5} - \sqrt{3} - \sqrt{5}| = |- \sqrt{3}| = \sqrt{3}$ .

Vậy đáp án là C.

Nhận xét: Học sinh có thể mắc sai lầm khi tính $y = f (x) = x - \sqrt{5}$ , từ đó dẫn đến việc tính $f (\sqrt{5} - \sqrt{3}) = - \sqrt{3}$ và chọn D. Hoặc tính nhầm thành $y = f (x) = x + \sqrt{5}$ sẽ dẫn đến $f (\sqrt{5} - \sqrt{3}) = 2 \sqrt{5} - \sqrt{3}$ , từ đó chọn A. Hoặc cũng có thể tính thành $y = f (x) = - (x + \sqrt{5})$ , dẫn đến $f (\sqrt{5} - \sqrt{3}) = - 2 \sqrt{5} + \sqrt{3}$ . Đáp án là B.

Câu 4:

Xét tính chẵn, lẻ của hai hàm số $f (x) = - |x|$ và $g (x) = |x + 1| - |x - 1|$ .

A. f(x) là hàm số chẵn, g(x) là hàm số chẵn

B. f(x)là hàm số lẻ, g(x) là hàm số chẵn

C. f(x) là hàm số lẻ, g(x) là hàm số lẻ

D. f(x) là hàm số chẵn, g(x) là hàm số lẻ

Xem đáp án

Tập xác định của hàm số f(x)và g(x) đều là $ℝ$ .

Với $x \in ℝ$ thì $- x \in ℝ$ và ta có: $f (- x) = - |- x| = - |x| = f (x)$ ;

$g (- x) = |- x + 1| - |- x - 1| = |x - 1| - |x + 1| = - g (x)$ .

Vậy f(x)là hàm số chẵn, g(x) là hàm số lẻ. Đáp án là D.

Câu 5:

Xét tính đồng biến và nghịch biến của hàm số $y = f (x) = - x^{2} + 4 x - 2$ trên các khoảng $(- \infty; 2)$ và $(2; + \infty)$ .

A. $f (x)$ đồng biến trên khoảng $(- \infty; 2)$ và nghịch biến trên khoảng $(2; + \infty)$

B. $f (x)$ đồng biến trên cả hai khoảng $(- \infty; 2)$ và $(2; + \infty)$

C. $f (x)$ nghịch biến trên khoảng $(- \infty; 2)$ và đồng biến trên khoảng $(2; + \infty)$

D. $f (x)$ nghịch biến trên cả hai khoảng $(- \infty; 2)$ và $(2; + \infty)$

Xem đáp án

Với $x_{1} \neq x_{2}$ ta có:

$\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} = \frac{(- {x_{2}}^{2} + 4 x_{2} - 2) - (- {x_{1}}^{2} + 4 x_{1} - 2)}{x_{2} - x_{1}} = \frac{- ({x_{2}}^{2} - {x_{1}}^{2}) + 4 (x_{2} - x_{1})}{x_{2} - x_{1}} = - (x_{2} + x_{1}) + 4$ .

· Với $x_{1}, x_{2} \in (- \infty; 2)$ thì x₁ < 2; x₂ <2 nên $x_{1} + x_{2} < 4 \Rightarrow - (x_{1} + x_{2}) + 4 > 0$ nên f(x) đồng biến trên khoảng $(- \infty; 2)$ .

· · Với $x_{1}, x_{2} \in (2; + \infty)$ thì x₁>2; x₂ >2 nên $x_{1} + x_{2} > 4 \Rightarrow - (x_{1} + x_{2}) + 4 < 0$ nên f(x) nghịch biến trên khoảng $(2; + \infty)$ .

Vậy đáp án là A.

Nhận xét: Với 4 phương án trả lời cho ta biết f(x) đồng biến hoặc nghịch biến trên mỗi khoảng $(- \infty; 2)$ và $(2; + \infty)$ .

Vì vậy, ta lấy hai giá trị bất kì $x_{1} < x_{2}$ thuộc mỗi khoảng rồi so sánh $f (x_{1})$ và $f (x_{2})$ . Chẳng hạn $x_{1} = 0; x_{2} = 1$ có $f (0) = - 2$ ; $f (1) = 1$ nên $f (0) < f (1)$ , suy ra f(x) đồng biến trên khoảng $(- \infty; 2)$ .

Câu 6:

Tập xác định của hàm số $y = \sqrt{x + 1} + 3 \sqrt{2 - x}$ là:

A. $D = (- 2; 0) \cup (2; + \infty)$

B. $D = [- 1; 2]$

C. $D = (- \infty; 2]$

D. $D = [2; + \infty)$

Xem đáp án

Đáp án B

Điều kiện xác định của hàm số : $\{\begin{cases} x + 1 \geq 0 \\ 2 - x \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq - 1 \\ x \leq 2 \end{cases} \Leftrightarrow - 1 \leq x \leq 2$

Do đó, tập xác định của hàm số $y = \sqrt{x + 1} + 3 \sqrt{2 - x}$ là:D=[-1; 2].

Câu 7:

Tập xác định của hàm số $y = \sqrt{2 x + 1} + \frac{1}{3 |x| - 1}$ là:

A. $D = ℝ \ \{- \frac{1}{3}; \frac{1}{3}\}$

B. $D = (- \infty; - \frac{1}{2})$

C. $D = [- \frac{1}{2}; + \infty) \ \{- \frac{1}{3}; \frac{1}{3}\}$

D. $D = (- \frac{1}{2}; + \infty) \ \{- \frac{1}{3}; \frac{1}{3}\}$

Xem đáp án

Điều kiện xác định của hàm số:

$\{\begin{cases} 2 x + 1 \geq 0 \\ 3 |x| - 1 \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq - \frac{1}{2} \\ |x| \neq \frac{1}{3} \end{cases} \Leftrightarrow \{\begin{cases} x \geq - \frac{1}{2} \\ x \neq \pm \frac{1}{3} \end{cases}$

Suy ra,tập xác định của hàm số $y = \sqrt{2 x + 1} + \frac{1}{3 |x| - 1}$ là: $D = [- \frac{1}{2}; + \infty) \ \{- \frac{1}{3}; \frac{1}{3}\}$

Câu 8:

Cho hàm số $y = f (x) = \{\begin{cases} 3 x n ế u x < 0 \\ x^{2} + 2 n ế u x \geq 0 \end{cases}$ . Khi đó:

A. f(-1) = 3

B. f(-2) = 6

C. f(2) = 6

D. f(0) = 0

Xem đáp án

Ta có: f(-1) = 3.(-1) = -3

f(-2)= 3.(-2) = -6

f(2) = 2² + 2 = 6

f(0) = 0² + 2 = 2

Chọn C

Câu 9:

Tìm m để hàm số $f (x) = \frac{x}{x - m}$ xác định trên khoảng (0;5).

A. 0 < m < 5

B. $m \leq 0$

C. $m \geq 5$

D. $m \leq 0$ hoặc $m \geq 5$

Xem đáp án

Hàm số $f (x) = \frac{x}{x - m}$ xác định khi $x \neq m$ .

Do đó, để hàm số đã cho xác định trên khoảng (0 ; 5) thì $m \notin (0; 5)$ . Do đó $m \leq 0$ hoặc $m \geq 5$ .

Câu 10:

Hàm số $y = \frac{2 x + 1}{x - 1}$ nghịch biến trên khoảng nào sau đây?

A. $(1; + \infty)$

B. $(- \frac{1}{2}; + \infty)$

C. $(- \infty; 2)$

D. $(- 1; \frac{3}{2})$

Xem đáp án

Tập xác định của hàm số là $D = ℝ \ \{1\}$ .

Nhận thấy số 1 thuộc các khoảng $(- \frac{1}{2}; + \infty); (- \infty; 2); (- 1; \frac{3}{2})$ nên các đáp án B, C, D đều sai.

Câu 11:

Tìm m để hàm số $y = \frac{m}{x + 2}$ luôn nghịch biến trong khoảng xác định của nó.

A. m > 0

B. m < 0

C. m = 0

D. m > -2

Xem đáp án

Tập xác định : D= R\ {-2}.

Lấy $x_{1} \neq x_{2}$ , khi đó ta có:

$\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} = \frac{\frac{m}{x_{2} + 2} - \frac{m}{x_{1} + 2}}{x_{2} - x_{1}} = \frac{\frac{m (x_{1} + 2) - m (x_{2} + 2)}{(x_{2} + 2) . (x_{1} + 2)}}{x_{2} - x_{1}} = \frac{m (x_{1} - x_{2})}{(x_{2} + 2) (x_{1} + 2) (x_{2} - x_{1})} = \frac{- m}{(x_{2} + 2) (x_{1} + 2)}$

Với $x_{1}; x_{2}$ thuộc $(- 2; + \infty)$ hoặc cùng thuộc $(- \infty; - 2)$ thì $(x_{1} + 2) (x_{2} + 2) > 0$

Vì vậy f(x) nghịch biến khi $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} < 0 \Leftrightarrow - m < 0 \Leftrightarrow m > 0$ .

Câu 12:

Hàm số nào là hàm số lẻ

A. $y = x^{2} - 2 x$

B. $y = x^{3} + x$

C. $y = x^{2} + |x|$

D. $y = x^{3} - x^{2}$

Xem đáp án

Đáp án B

Xét hàm số y = x³ +x

Tập xác định : D= R

$\forall x \in D \Rightarrow - x \in D$

Ta có: f(-x) = (-x)³ + (- x) = -x³ – x = - f(x)

Do đó, hàm số y= x³ + x là hàm số lẻ.

Câu 13:

Hàm số nào có tập xác định D= R.

A. $y = \frac{2 x + 3}{x - 1}$

B. $y = \frac{2 x + 3}{\sqrt{4 x - 8}}$

C. $y = \frac{10 x - 20}{\sqrt{x^{2} + 1}}$

D. $y = |2 x + 4| + \sqrt{x^{2} - 16}$

Xem đáp án

* Hàm số $y = \frac{2 x + 3}{x - 1}$ có điều kiện là: $x \neq 1$ nên tập xác định: D= R\{1}.

* Hàm số $y = \frac{2 x + 3}{\sqrt{4 x - 8}}$ có điều kiện: 4x – 8 > 0 hay x> 2 nên tập xác định $D = (2; + \infty)$ .

* Hàm số $y = \frac{10 x - 20}{\sqrt{x^{2} + 1}}$ có điều kiện x² + 1 >0 ( luôn đúng với mọi x vì $x^{2} \geq 0$ ) nên tập xác định của hàm số này là D= R.

* Hàm số $y = |2 x + 4| + \sqrt{x^{2} - 16}$ có điều kiện là: $x^{2} - 16 \geq 0 \Leftrightarrow (x + 4) (x - 4) \geq 0 \Leftrightarrow [\begin{array}{l} x \leq - 4 \\ x \geq 4 \end{array}$

nên tập xác định là: $(- \infty; - 4] \cup [4; + \infty)$

Câu 14:

Trong các hình vẽ sau, hình nào minh họa đồ thị hàm số chẵn?

A.

B.

C.

D.

Xem đáp án

Vì đồ thị hàm số chẵn nhận trục tung làm trục đối xứng nên phương án C đúng.

Câu 15:

Trong các hình sau, hình nào minh họa đồ thị của một hàm số lẻ?

A.

B.

C.

D.

Xem đáp án

Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng nên phương án B đúng.

Câu 16:

Trong các điểm M( -1; 5); N(1; 4); P(2; 0); Q(3; 1), điểm nào thuộc đồ thị hàm số $y = x^{2} - 2 x + 5$

A. Điểm M

B. Điểm N

C. Điểm P

D. Điểm Q

Xem đáp án

Thay tọa độ từng điểm vào công thức hàm số, nếu được đẳng thức đúng thì điểm đó thuộc đồ thị.

* Với điểm M (-1;5), ta thay x = -1; y = 5 vào công thức $y = x^{2} - 2 x + 5$ , nhận thấy

$5 \neq {(- 1)}^{2} - 2 . (- 1) + 5$ nên M không thuộc đồ thị hàm số.

* Với N (1; 4) ta được:

4= 1² – 2.1 + 5 nên điểm N thuộc đồ thị hàm số.

* Với P(2; 0) ta được:

$0 \neq 2^{2} - 2.2 + 5$ nên điểm P không thuộc đồ thị hàm số.

* Với điểm Q(3; 1) ta được:

$1 \neq 3^{2} - 2.3 + 5$ nên điểm Q không thuộc đồ thị hàm số.

Câu 17:

Cho hàm số $y = f (x)$ có đồ thị như hình vẽ bên.

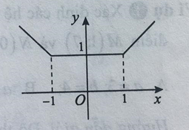
Khẳng định nào sau đây là đúng?

A. $f (x)$ đồng biến trên khoảng $(- \infty; - 1)$

B. $f (x)$ nghịch biến trên khoảng $(- \infty; 0)$

C. $f (x)$ đồng biến trên khoảng $(1; + \infty)$

D. $f (x)$ nghịch biến trên khoảng $(- 1; 1)$

Xem đáp án

Quan sát đồ thị, theo chiều từ trái sang phải; nếu đồ thị đi lên (hoặc đi xuống) trong khoảng nào đó thì hàm số sẽ đồng biến (hoặc nghịch biến) trong khoảng này.

Ta thấy:

+ Trên khoảng $(- \infty; - 1)$ đồ thị hàm số đi xuống nên hàm số nghịch biến.

+ Trên khoảng ( -1; 1) thì giá trị của hàm số không đổi y = 1 nên hàm số không đồng biến, không nghịch biến.

+ Trên khoảng $(1; + \infty)$ đồ thị hàm số đi lên nên hàm số đồng biến.

Câu 18:

Hàm số nào sau đây không chẵn, không lẻ ?

A. $y = x^{4} - 1$

B. $y = x^{3} - 3 x$

C. $y = \frac{1}{x + 3}$

D. $y = |2 x|$

Xem đáp án

Tập xác định của hàm số $y = \frac{1}{x + 3}$ là $D = ℝ \ \{- 3\}$ .

Nhận thấy 3 $\in$ D, nhưng -3 $\notin$ D.

Vậy hàm số $y = \frac{1}{x + 3}$ không chẵn và không lẻ.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Hàm số có đáp án

Hàm số

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương