Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây sai?
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: D
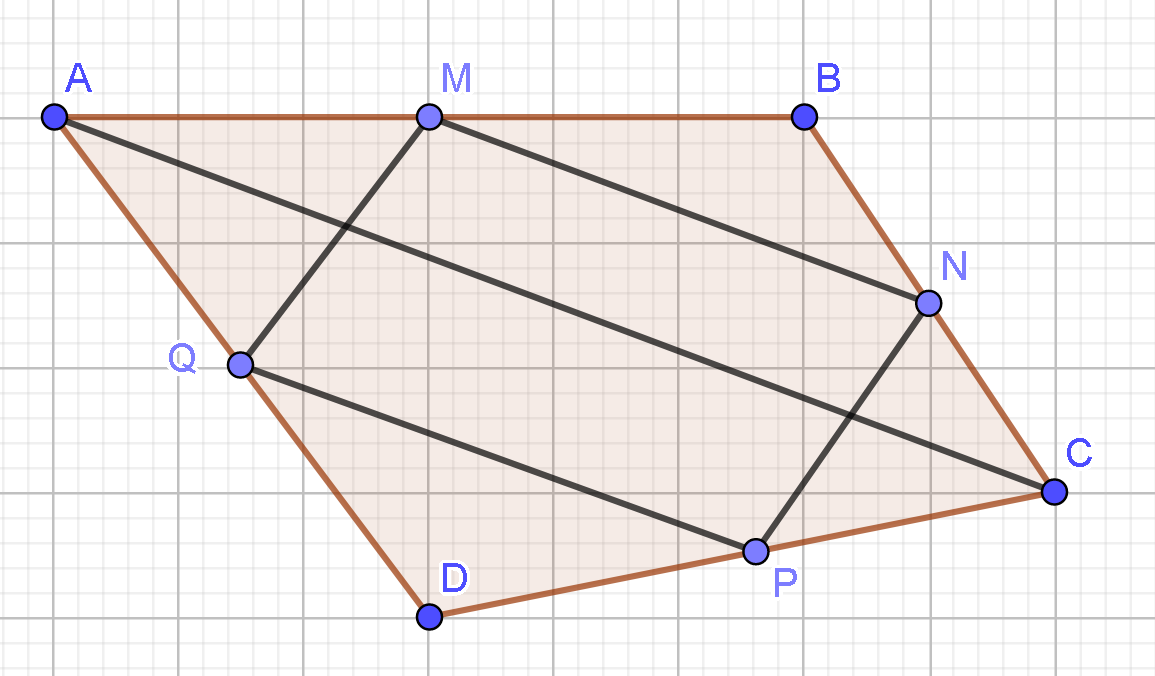
Ta có: (do cùng song song và bằng ).
Do đó MNPQ là hình bình hành.
Vì MNPQ là hình bình hành nên
Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho . Gọi K là trung điểm của MN. Khi đó :
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
Tam giác ABC có . Gọi D là chân đường phân giác trong góc . Khi đó góc bằng bao nhiêu độ?
Cho tam giác ABC, có bao nhiêu vectơ khác vectơ - không, có điểm đầu và điểm cuối là các đỉnh A, B, C.
Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:
Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu -
Tam giác ABC có . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.