30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Ôn tập chương 4 có đáp án

Câu 1:

Tam giác ABC có $A B = 5, B C = 7, C A = 8$ . Số đo góc $\hat{A}$ bằng:

A. $30 °;$

B. $45 °;$

C. $60 °;$

D. $90 °;$

Đáp án đúng là: C

Theo định lí hàm cosin, ta có: $\cos \hat{A} = \frac{A B^{2} + A C^{2} - B C^{2}}{2 A B . A C} = \frac{5^{2} + 8^{2} - 7^{2}}{2.5.8} = \frac{1}{2}$ .

Do đó, $\hat{A} = 60 °$ .

Câu 2:

Tam giác ABC có $A C = 4, \hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 8$

B. $S_{Δ A B C} = 4 \sqrt{3}$

C. $S_{Δ A B C} = 4$

D. $S_{Δ A B C} = 8 \sqrt{3}$

Xem đáp án

Đáp án đúng là: C

Ta có: $\hat{A B C} = 180^{0} - (\hat{B A C} + \hat{A C B}) = 75 ° = \hat{A C B} .$

Suy ra tam giác ABC cân tại A nên $A B = A C = 4$

Diện tích tam giác ABC là $S_{Δ A B C} = \frac{1}{2} A B . A C \sin \hat{B A C} = 4$ (đơn vị diện tích)

Câu 3:

Cho tam giác ABC, có bao nhiêu vectơ khác vectơ - không, có điểm đầu và điểm cuối là các đỉnh A, B, C.

A. 3

B. 6

C. 4

D. 9

Xem đáp án

Đáp án đúng là: B

Đó là các vectơ: $\vec{A B}, \vec{B A}, \vec{B C}, \vec{C B}, \vec{C A}, \vec{A C} .$

Câu 4:

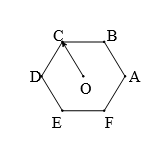
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ - không, cùng phương với $\vec{O C}$ có điểm đầu và điểm cuối là các đỉnh của lục giác là

A. 4

B. 6

C. 7

D. 9

Xem đáp án

Đáp án đúng là: B

Đó là các vectơ: $\vec{A B}, \vec{B A}, \vec{D E}, \vec{E D}, \vec{F C}, \vec{C F}$ .

Câu 5:

Tam giác ABC có $A B = \sqrt{2}, A C = \sqrt{3}$ và $\hat{C} = 45 °$ . Tính độ dài cạnh BC.

A. $B C = \sqrt{5};$

B. $B C = \frac{\sqrt{6} + \sqrt{2}}{2};$

C. $B C = \frac{\sqrt{6} - \sqrt{2}}{2};$

D. $B C = \sqrt{6};$

Xem đáp án

Đáp án đúng là: B

Theo định lí hàm cosin, ta có:

$A B^{2} = A C^{2} + B C^{2} - 2. A C . B C . \cos \hat{C}$

$\Rightarrow {(\sqrt{2})}^{2} = {(\sqrt{3})}^{2} + B C^{2} - 2. \sqrt{3} . B C . \cos 45 °$

- $\Rightarrow B C^{2} - \sqrt{6}$ .BC + 1 = 0

$\Rightarrow B C = \frac{\sqrt{6} + \sqrt{2}}{2}$ .

Câu 6:

Cho hình vuông ABCD. Khẳng định nào sau đây đúng?

A. $\vec{A C} = \vec{B D};$

B. $\vec{A B} = \vec{C D};$

C. $|\vec{A B}| = |\vec{B C}|;$

D. Hai vectơ $\vec{A B}, \vec{A C}$ cùng hướng.

Xem đáp án

Đáp án đúng là: C

Vì $A B = B C \Leftrightarrow |\vec{A B}| = |\vec{B C}| .$

Câu 7:

Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.

A. $h = 3 \sqrt{3}$

B. $h = \sqrt{3}$

C. $h = 3$

D. $h = \frac{3}{2}$

Xem đáp án

Đáp án đúng là: C

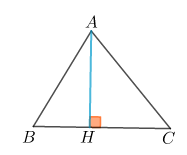
Áp dụng định lý hàm số cosin, ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C \cos A = 27 \Rightarrow B C = 3 \sqrt{3}$ (đơn vị độ dài).

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 60^{0} = \frac{9 \sqrt{3}}{2}$ (đơn vị diện tích).

Lại có $S_{Δ A B C} = \frac{1}{2} . B C . h_{a} \Rightarrow h_{a} = \frac{2 S}{B C} = 3$ (đơn vị độ dài).

Câu 8:

Cho $\vec{a}$ và $\vec{b}$ là các vectơ khác $\vec{0}$ với $\vec{a}$ là vectơ đối của $\vec{b}$ . Khẳng định nào sau đây sai?

A. Hai vectơ

\vec{a}, \vec{b}

cùng phương;

B. Hai vectơ

\vec{a}, \vec{b}

ngược hướng;

C. Hai vectơ

\vec{a}, \vec{b}

cùng độ dài;

D. Hai vectơ

\vec{a}, \vec{b}

chung điểm đầu.

Xem đáp án

Đáp án đúng là: D

Ta có : $\vec{a} = - \vec{b}$ . Do đó, $\vec{a}$ và $\vec{b}$ cùng phương, cùng độ dài và ngược hướng nhau.

Câu 9:

Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để $\vec{A B} = \vec{C D}$ ?

A. ABCD là hình bình hành.

B. ABCD là hình tứ giác

C. AC = BD

D. AB = CD

Xem đáp án

Đáp án đúng là : A

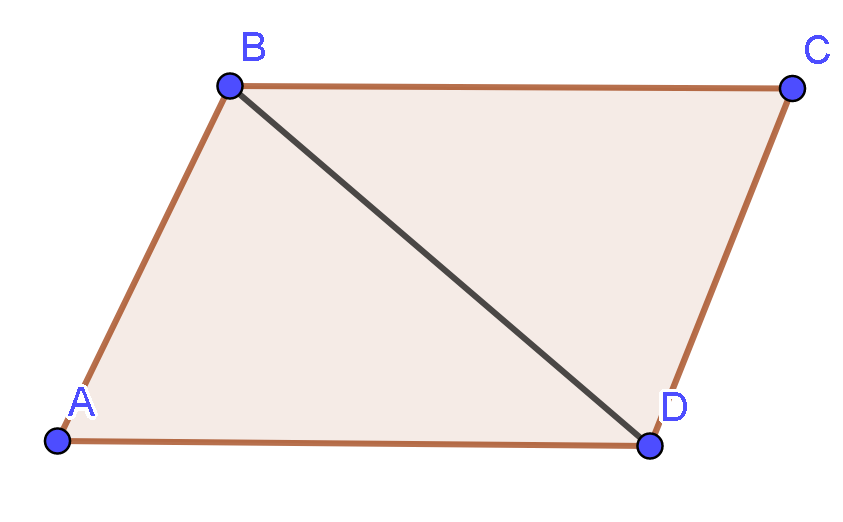
Ta có:

$\vec{A B} = \vec{C D} \Rightarrow \{\begin{cases} A B ∥ C D \\ A B = C D \end{cases} \Rightarrow A B D C$ là hình bình hành.

Mặt khác, ABCD là hình bình hành $\Rightarrow \{\begin{cases} A B ∥ C D \\ A B = C D \end{cases}$ và $\vec{A B}; \vec{D C}$ cùng hướng $\Rightarrow \vec{A B} = \vec{C D}$ .

Do đó, điều kiện cần và đủ để $\vec{A B} = \vec{C D}$ là ABCD là hình bình hành.

Câu 10:

Cho hình thoi ABCD cạnh bằng 1cm và có $\hat{B A D} = 60 °$ . Tính độ dài AC.

A. $A C = \sqrt{3};$

B. $A C = \sqrt{2}$

C. $A C = 2 \sqrt{3};$

D. $A C = 2$

Xem đáp án

Đáp án đúng là: A

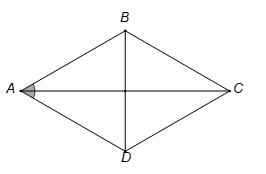
Do ABCD là hình thoi, có $\hat{B A D} = 60 ° \Rightarrow \hat{A B C} = 120 °$ .

Theo định lí hàm cosin, ta có:

$A C^{2} = A B^{2} + B C^{2} - 2. A B . B C . \cos \hat{A B C}$

$\Rightarrow 1^{2} + 1^{2} - 2.1.1. \cos 120 ° = 3 \Rightarrow A C = \sqrt{3}$

Câu 11:

Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:

A. $|3 \vec{O A} + 4 \vec{O B}| = 5 a;$

B. $|2 \vec{O A}| + |3 \vec{O B}| = 5 a;$

C. $|7 \vec{O A} - 2 \vec{O B}| = 5 a;$

D. $|11 \vec{O A}| - |6 \vec{O B}| = 5 a .$

Xem đáp án

Đáp án đúng là: C

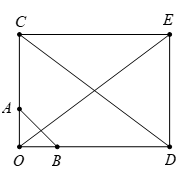
Dựa vào các đáp án, ta có nhận xét sau:

- Gọi C nằm trên tia đối của tia AO sao cho

$O C = 3 O A$ $\Rightarrow 3 \vec{O A} = \vec{O C} .$

Và D nằm trên tia đối của tia BO sao cho

$O D = 4 O B$ $\Rightarrow 4 \vec{O B} = \vec{O D} .$

Dựng hình chữ nhật OCED suy ra $\vec{O C} + \vec{O D} = \vec{O E}$ (quy tắc hình bình hành).

Ta có: $|3 \vec{O A} + 4 \vec{O B}| = |\vec{O C} + \vec{O D}| = |\vec{O E}| = O E = C D = \sqrt{O C^{2} + O D^{2}} = 5 a .$

Do đó, A đúng

- B đúng, vì $|2 \vec{O A}| + |3 \vec{O B}| = 2 |\vec{O A}| + 3 |\vec{O B}| = 2 a + 3 a = 5 a .$

- D đúng, vì $|11 \vec{O A}| - |6 \vec{O B}| = 11 |\vec{O A}| - 6 |\vec{O B}| = 11 a - 6 a = 5 a .$

Vậy chỉ còn đáp án C.

Câu 12:

Cho tam giác ABC cân ở A, đường cao AH. Khẳng định nào sau đây sai?

A. $\vec{A B} = \vec{A C};$

B. $\vec{H C} = - \vec{H B};$

C. $|\vec{A B}| = |\vec{A C}|;$

D. $\vec{B C} = 2 \vec{H C} .$

Xem đáp án

Đáp án đúng là : A

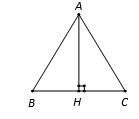
Tam giác ABC cân ở A, đường cao AH. Do đó, H là trung điểm BC (tính chất tam giác cân).

Ta có:

- $A B = A C \Rightarrow |\vec{A B}| = |\vec{A C}|$ . Do đó, B đúng.

- H là trung điểm $B C \Rightarrow \{\begin{cases} \vec{H C} = - \vec{H B} \\ \vec{B C} = 2 \vec{H C} \end{cases}$ . Do đó, C, D đúng.

Câu 13:

Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho $3 \vec{A M} = 2 \vec{A B}$ và $3 \vec{D N} = 2 \vec{D C} .$ Tính vectơ $\vec{M N}$ theo hai vectơ

A. $\vec{M N} = \frac{1}{3} \vec{A D} + \frac{1}{3} \vec{B C};$

B. $\vec{M N} = \frac{1}{3} \vec{A D} - \frac{2}{3} \vec{B C};$

C. $\vec{M N} = \frac{1}{3} \vec{A D} + \frac{2}{3} \vec{B C};$

D. $\vec{M N} = \frac{2}{3} \vec{A D} + \frac{1}{3} \vec{B C} .$

Xem đáp án

Đáp án đúng là: C

Ta có : $\vec{M N} = \vec{M A} + \vec{A D} + \vec{D N}$ và $\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N} .$

Suy ra $3 \vec{M N} = \vec{M A} + \vec{A D} + \vec{D N} + 2 (\vec{M B} + \vec{B C} + \vec{C N})$

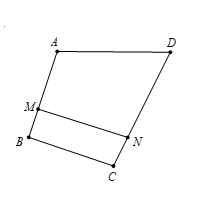
$= (\vec{M A} + 2 \vec{M B}) + \vec{A D} + 2 \vec{B C} + (\vec{D N} + 2 \vec{C N}) .$

Theo bài ra, ta có: $\vec{M A} + 2 \vec{M B} = \vec{0}$ và $\vec{D N} + 2 \vec{C N} = \vec{0} .$ Thật vậy:

$3 \vec{A M} = 2 \vec{A B} \Leftrightarrow 3 \vec{A M} = 2 (\vec{A M} + \vec{M B})$

$\Leftrightarrow 3 \vec{A M} = 2 \vec{A M} + 2 \vec{M B}$

$\Leftrightarrow \vec{A M} = 2 \vec{M B}$

$\Leftrightarrow 2 \vec{M B} - \vec{A M} = 0$

$\Leftrightarrow 2 \vec{M B} + \vec{M A} = 0$

$3 \vec{D N} = 2 \vec{D C} \Leftrightarrow 3 \vec{D N} = 2 (\vec{D N} + \vec{N C})$

$\Leftrightarrow 3 \vec{D N} = 2 \vec{D N} + 2 \vec{N C}$

$\Leftrightarrow \vec{D N} = 2 \vec{N C}$

$\Leftrightarrow \vec{D N} - 2 \vec{N C} = 0$

$\Leftrightarrow \vec{D N} + 2 \vec{C N} = 0$

Vậy $3 \vec{M N} = \vec{A D} + 2 \vec{B C} \Leftrightarrow \vec{M N} = \frac{1}{3} \vec{A D} + \frac{2}{3} \vec{B C} .$

Câu 14:

Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu $\vec{A D}$ - $\vec{A B}$ :

A. $\vec{A D}$

B. $\vec{C B}$

C. $\vec{A B}$

D. $\vec{B D}$

Xem đáp án

Đáp án đúng là: D

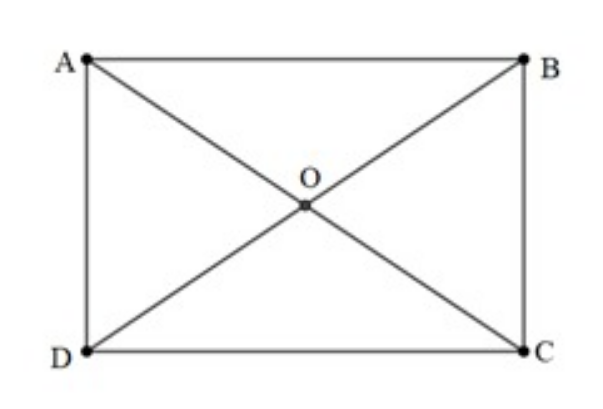
Áp dụng quy tắc 3 điểm cho A, B, D ta có: $\vec{A D}$ - $\vec{A B}$ = $\vec{B D}$ .

Câu 15:

Tam giác ABC có $A B = \frac{\sqrt{6} - \sqrt{2}}{2}, B C = \sqrt{3}, C A = \sqrt{2}$ . Gọi D là chân đường phân giác trong góc . Khi đó góc bằng bao nhiêu độ?

A. $45 °;$

B. $60 °;$

C. $75 °;$

D. $90 °;$

Xem đáp án

Đáp án đúng là: C

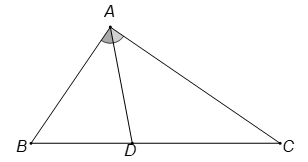
Theo định lí hàm cosin, ta có:

$\cos \hat{B A C} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = - \frac{1}{2}$

$\Rightarrow \hat{B A C} = 120 ° \Rightarrow \hat{B A D} = 60 °$

$\cos \hat{A B C} = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{\sqrt{2}}{2} \Rightarrow \hat{A B C} = 45 °$

Trong $Δ A B D$ có $\hat{B A D} = 60 °, \hat{A B D} = 45 ° \Rightarrow \hat{A D B} = 75 °$ .

Câu 16:

Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng ?

A. $\vec{D M} = \frac{1}{2} \vec{C D} + \vec{B C};$

B. $\vec{D M} = \frac{1}{2} \vec{C D} - \vec{B C};$

C. $\vec{D M} = \frac{1}{2} \vec{D C} - \vec{B C};$

D. $\vec{D M} = \frac{1}{2} \vec{D C} + \vec{B C} .$

Xem đáp án

Đáp án đúng là: C

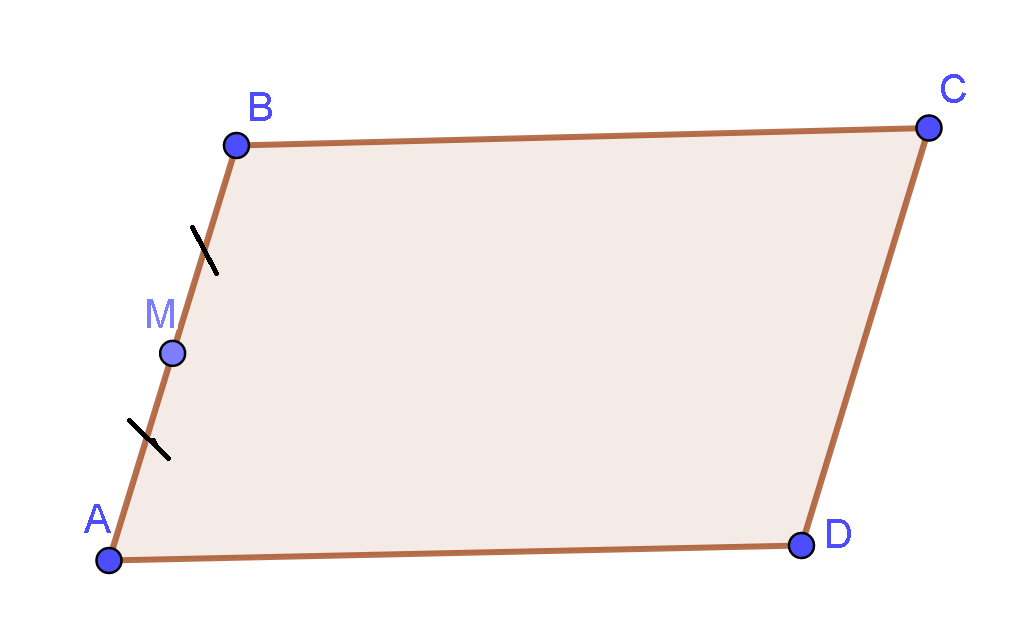
Xét các đáp án ta thấy cần phân tích vectơ $\vec{D M}$ theo hai vectơ $\vec{D C}$ và $\vec{B C} .$

Vì ABCD là hình bình hành nên $\vec{D B} = \vec{D A} + \vec{D C} .$

Và M là trung điểm AB nên $2 \vec{D M} = \vec{D A} + \vec{D B}$

$\Leftrightarrow 2 \vec{D M} = \vec{D A} + \vec{D A} + \vec{D C}$

$\Leftrightarrow 2 \vec{D M} = 2 \vec{D A} + \vec{D C} .$

$\Leftrightarrow 2 \vec{D M} = - 2 \vec{B C} + \vec{D C}$ suy ra $\vec{D M} = \frac{1}{2} \vec{D C} - \vec{B C} .$

Câu 17:

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây sai?

A. $\vec{M N} = \vec{Q P};$

B. $|\vec{Q P}| = |\vec{M N}|;$

C. $\vec{M Q} = \vec{N P};$

D. $|\vec{M N}| = |\vec{A C}| .$

Xem đáp án

Đáp án đúng là: D

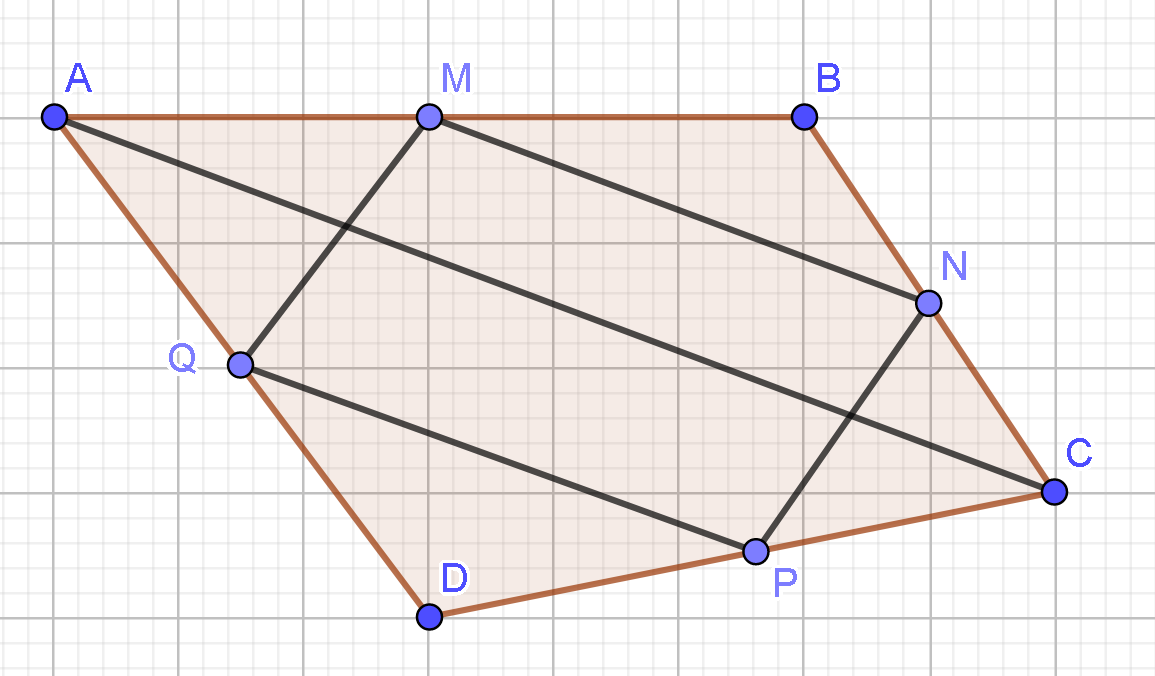
Ta có: $\{\begin{cases} M N ∥ P Q \\ M N = P Q \end{cases}$ (do cùng song song và bằng $\frac{1}{2} A C$ ).

Do đó MNPQ là hình bình hành.

Vì MNPQ là hình bình hành nên $\vec{M N} = \vec{Q P};$ $|\vec{Q P}| = |\vec{M N}|;$ $\vec{M Q} = \vec{N P} .$

Câu 18:

Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:

A. ${50 cm}^{2}$

B. $50 \sqrt{2} {cm}^{2}$

C. ${75 cm}^{2}$

D. $15 \sqrt{105} {cm}^{2}$

Xem đáp án

Đáp án đúng là: C

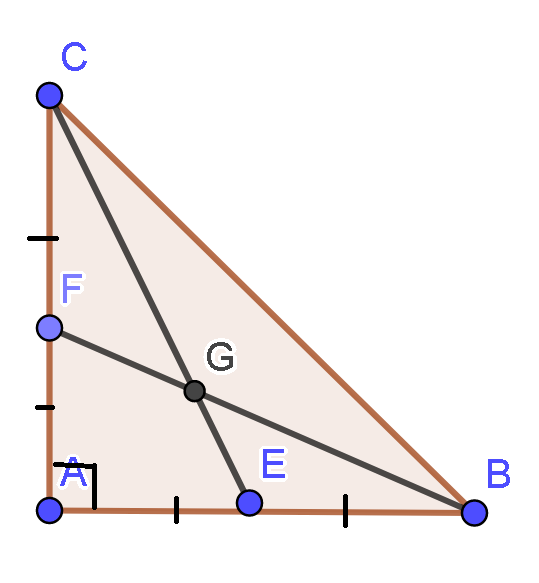
Vì F là trung điểm của AC $F C = \frac{1}{2} A C = 15 c m .$

Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.

Khi đó: $\frac{d (B; (A C))}{d (G; (A C))} = \frac{B F}{G F} = 3 \Rightarrow d (G; (A C)) = \frac{1}{3} d (B; (A C)) = \frac{A B}{3} = 10 c m .$

Vậy diện tích tam giác GFC là: $S_{Δ G F C} = \frac{1}{2} . d (G; (A C)) . F C = \frac{1}{2} .10.15 = 75 c m^{2} .$

Câu 19:

Cho tam giác ABC đều cạnh a. Tính $|\vec{A B} + \vec{A C}| .$

A. $|\vec{A B} + \vec{A C}| = a \sqrt{3};$

B. $|\vec{A B} + \vec{A C}| = \frac{a \sqrt{3}}{2};$

C. $|\vec{A B} + \vec{A C}| = 2 a;$

D. $|\vec{A B} + \vec{A C}| = 2 a \sqrt{3};$

Xem đáp án

Đáp án đúng là: A

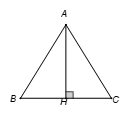
Gọi H là trung điểm của $B C \Rightarrow A H ⊥ B C .$

Xét tam giác vuông AHC ta có:

$A H^{2} + H C^{2} = A C^{2}$

$\Leftrightarrow A H = \sqrt{A C^{2} - H C^{2}}$

$\Leftrightarrow A H = \sqrt{a^{2} - \frac{a^{2}}{4}}$

Suy ra

$A H = \frac{B C \sqrt{3}}{2} = \frac{a \sqrt{3}}{2} .$

Ta lại có $|\vec{A B} + \vec{A C}| = |\vec{A H} + \vec{H B} + \vec{A H} + \vec{H C}| = |2 \vec{A H}|$

Suy ra : $|2 \vec{A H}| = 2. \frac{a \sqrt{3}}{2} = a \sqrt{3}$

Câu 20:

Cho tam giác ABC có M là trung điểm của BC. Tính

\vec{A B}

theo

\vec{A M}

và

\vec{B C}

A. $\vec{A B} = \vec{A M} + \frac{1}{2} \vec{B C};$

B. $\vec{A B} = \vec{B C} + \frac{1}{2} \vec{A M};$

C. $\vec{A B} = \vec{A M} - \frac{1}{2} \vec{B C};$

D. $\vec{A B} = \vec{B C} - \frac{1}{2} \vec{A M};$

Xem đáp án

Đáp án đúng là: C

Ta có : $\vec{A B} = \vec{A M} + \vec{M B} = \vec{A M} - \frac{1}{2} \vec{B C} .$

Câu 21:

Cho góc $\hat{x O y} = 30 °$ . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:

A. $\frac{3}{2}$

B. $\sqrt{3};$

C. $2 \sqrt{2};$

D. 2

Xem đáp án

Đáp án đúng là: D

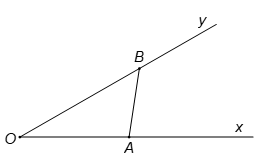
Theo định lí hàm sin, ta có:

$\frac{O B}{\sin \hat{O A B}} = \frac{A B}{\sin \hat{A O B}} \Leftrightarrow O B = \frac{A B}{\sin \hat{A O B}} . \sin \hat{O A B}$

$\Leftrightarrow \frac{1}{\sin 30 °} . \sin \hat{O A B} = 2 \sin \hat{O A B}$

Do đó, độ dài OB lớn nhất khi và chỉ khi

$\sin \hat{O A B} = 1 \Leftrightarrow \hat{O A B} = 90 °$ .

Khi đó OB = 2.

Câu 22:

Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho $N C = 2 N A$ . Gọi K là trung điểm của MN. Khi đó :

A. $\vec{A K} = \frac{1}{6} \vec{A B} + \frac{1}{4} \vec{A C} .$

B. $\vec{A K} = \frac{1}{4} \vec{A B} - \frac{1}{6} \vec{A C} .$

C. $\vec{A K} = \frac{1}{4} \vec{A B} + \frac{1}{6} \vec{A C} .$

D. $\vec{A K} = \frac{1}{6} \vec{A B} - \frac{1}{4} \vec{A C} .$

Xem đáp án

Đáp án đúng là: C

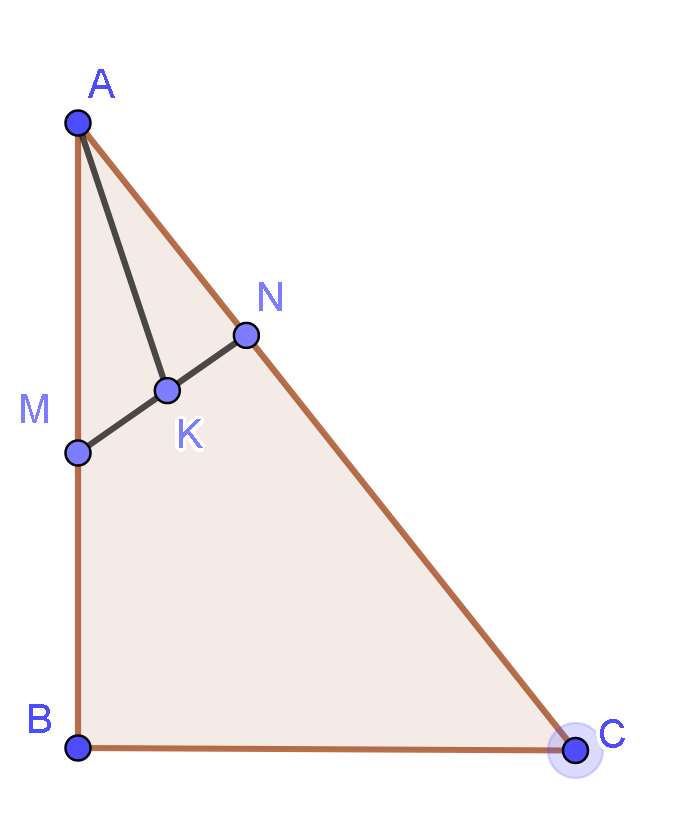
Vì K là trung điểm của MN nên ta có :

Ta có : $\vec{A K} = \frac{1}{2} (\vec{A M} + \vec{A N})$ .

Mà M là trung điểm của AB và N là điểm thuộc cạnh AC sao cho NC = 2AN nên ta có :

$\{\begin{cases} \vec{A M} = \frac{1}{2} \vec{A B} \\ \vec{A N} = \frac{1}{3} \vec{A C} \end{cases}$

Do đó, $\vec{A K} = \frac{1}{2} (\frac{1}{2} \vec{A B} + \frac{1}{3} \vec{A C}) = \frac{1}{4} \vec{A B} + \frac{1}{6} \vec{A C}$

Câu 23:

Cho hai vectơ $\vec{a}$ và $\vec{b}$ thỏa mãn $|\vec{a}| = |\vec{b}| = 1$ và hai vectơ $\vec{u} = \frac{2}{5} \vec{a} - 3 \vec{b}$ và $\vec{v} = \vec{a} + \vec{b}$ vuông góc với nhau. Xác định góc $α$ giữa hai vectơ $\vec{a}$ và $\vec{b}$ .

A. $α = 90^{0};$

B. $α = 180^{0};$

C. $α = 60^{0};$

D. $α = 45^{0};$

Xem đáp án

Đáp án đúng là: B

Ta có: $\vec{u} ⊥ \vec{v} \Rightarrow \vec{u} . \vec{v} = 0 \Leftrightarrow (\frac{2}{5} \vec{a} - 3 \vec{b}) (\vec{a} + \vec{b}) = 0 \Leftrightarrow \frac{2}{5} {\vec{a}}^{2} - \frac{13}{5} \vec{a} \vec{b} - 3 {\vec{b}}^{2} = 0$

$\overset{|\vec{a}| = |\vec{b}| = 1}{\to} \vec{a} \vec{b} = - 1.$

Suy ra $c o s (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = - 1 \Rightarrow (\vec{a}, \vec{b}) = 180^{0} .$

Câu 24:

Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng

\vec{A B} . \vec{B C} .

A. $\vec{A B} . \vec{B C} = a^{2};$

B. $\vec{A B} . \vec{B C} = \frac{a^{2} \sqrt{3}}{2};$

C. $\vec{A B} . \vec{B C} = - \frac{a^{2}}{2};$

D. $\vec{A B} . \vec{B C} = \frac{a^{2}}{2};$

Xem đáp án

Đáp án đúng là: C

Xác định được góc $(\vec{A B}, \vec{B C})$ là góc ngoài của góc $\hat{B}$ nên $(\vec{A B}, \vec{B C}) = 120^{0}$ (do tam giác ABC là tam giác đều nên góc $\hat{B} = 60 °$ , do đó, góc ngoài của góc B có số đo là 120^o).

Do đó $\vec{A B} . \vec{B C} = A B . B C . c o s (\vec{A B}, \vec{B C}) = a . a . c o s 120^{0} = - \frac{a^{2}}{2} .$

Câu 25:

Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu $\vec{C B}$ - $\vec{A B}$

A. $\vec{C B}$

B. $\vec{A B}$

C. $\vec{B A}$

D. $\vec{C A}$

Xem đáp án

Đáp án đúng là: D

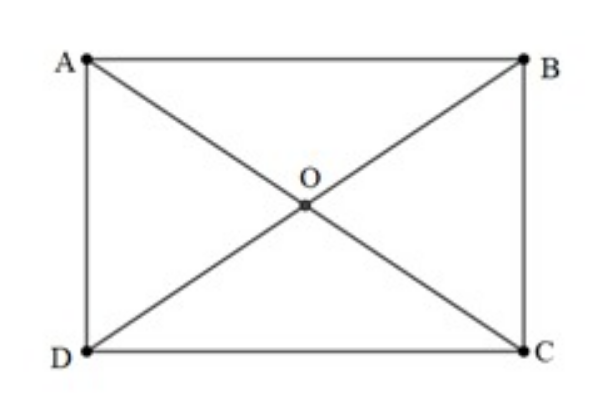
Ta có: $|\vec{B A}| = |\vec{A B}| = A B$ và $\vec{B A}$ ngược hướng với $\vec{A B} \Rightarrow$ $\vec{B A} = - \vec{A B}$

$\vec{C B} - \vec{A B} = \vec{C B} + (- \vec{A B}) = \vec{C B} + \vec{B A} = \vec{C A}$

Câu 26:

Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:

A. $13 {cm}^{2}$

B. $13 \sqrt{2} {cm}^{2}$

C. $12 \sqrt{3} {cm}^{2}$

D. $15 {cm}^{2}$

Xem đáp án

Đáp án đúng là: C

Xét tam giác ABC đều, có độ dài cạnh bằng a.

Theo định lí sin, ta có: $\frac{B C}{\sin \hat{B A C}} = 2 R \Leftrightarrow \frac{a}{\sin 60^{0}} = 2.4 \Leftrightarrow a = 8. \sin 60^{0} = 4 \sqrt{3}$ (đơn vị độ dài).

Vậy diện tích cần tính là:

$S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{B A C} = \frac{1}{2} . {(4 \sqrt{3})}^{2} . \sin 60^{0} = 12 \sqrt{3} c m^{2} .$

Câu 27:

Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?

A. $\vec{A B} . \vec{A C} = \frac{1}{2} a^{2};$

B. $\vec{A C} . \vec{C B} = - \frac{1}{2} a^{2};$

C. $\vec{G A} . \vec{G B} = \frac{a^{2}}{6};$

D. $\vec{A B} . \vec{A G} = \frac{1}{2} a^{2} .$

Xem đáp án

Đáp án đúng là: C

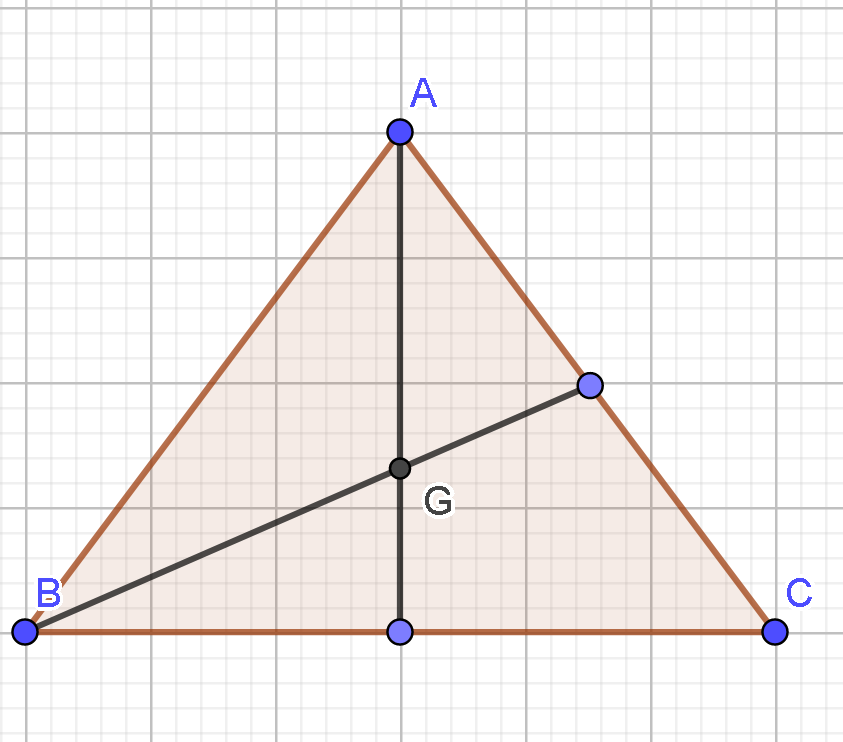
- Xác định được góc $(\vec{A B}, \vec{A C})$ là góc $\hat{A}$ nên $(\vec{A B}, \vec{A C}) = 60^{0} .$ (do tam giác ABC đều)

Do đó $\vec{A B} . \vec{A C} = A B . A C . c o s (\vec{A B}, \vec{A C}) = a . a . c o s 60^{0} = \frac{a^{2}}{2} ⇒$ A đúng

- Xác định được góc $(\vec{A C}, \vec{C B})$ là góc ngoài của góc $\hat{C}$ nên $(\vec{A C}, \vec{C B}) = 120^{0} .$

Do đó $\vec{A C} . \vec{C B} = A C . C B . c o s (\vec{A C}, \vec{C B}) = a . a . c o s 120^{0} = - \frac{a^{2}}{2} \Rightarrow$ B đúng.

Xác định được góc $(\vec{G A}, \vec{G B})$ là góc $\hat{A G B}$ nên $(\vec{G A}, \vec{G B}) = 120^{0} .$

Ta có: AG nằm trên đường trung tuyến cũng chính là đường cao của tam giác đều ABC, ta tính được đường cao, suy ra: AG = $\frac{2}{3}$ .a. $\frac{\sqrt{3}}{2}$ = $\frac{a}{\sqrt{3}}$ .

Tương tự, GB = $\frac{a}{\sqrt{3}}$ .

Do đó $\vec{G A} . \vec{G B} = G A . G B . c o s (\vec{G A}, \vec{G B}) = \frac{a}{\sqrt{3}} . \frac{a}{\sqrt{3}} . c o s 120^{0} = - \frac{a^{2}}{6} \Rightarrow$ C sai.

Xác định được góc $(\vec{A B}, \vec{A G})$ là góc $\hat{G A B}$ nên $(\vec{A B}, \vec{A G}) = 30^{0} .$

Do đó $\vec{A B} . \vec{A G} = A B . A G . c o s (\vec{A B}, \vec{A G}) = a . \frac{a}{\sqrt{3}} . c o s 30^{0} = \frac{a^{2}}{2} \Rightarrow$ D đúng.

Câu 28:

Cho tam giác ABC vuông tại A và có AB = c; AC = b. Tính

\vec{B A} . \vec{B C} .

A. $\vec{B A} . \vec{B C} = b^{2};$

B. $\vec{B A} . \vec{B C} = c^{2};$

C. $\vec{B A} . \vec{B C} = b^{2} + c^{2};$

D. $\vec{B A} . \vec{B C} = b^{2} - c^{2};$

Xem đáp án

Đáp án đúng là: B

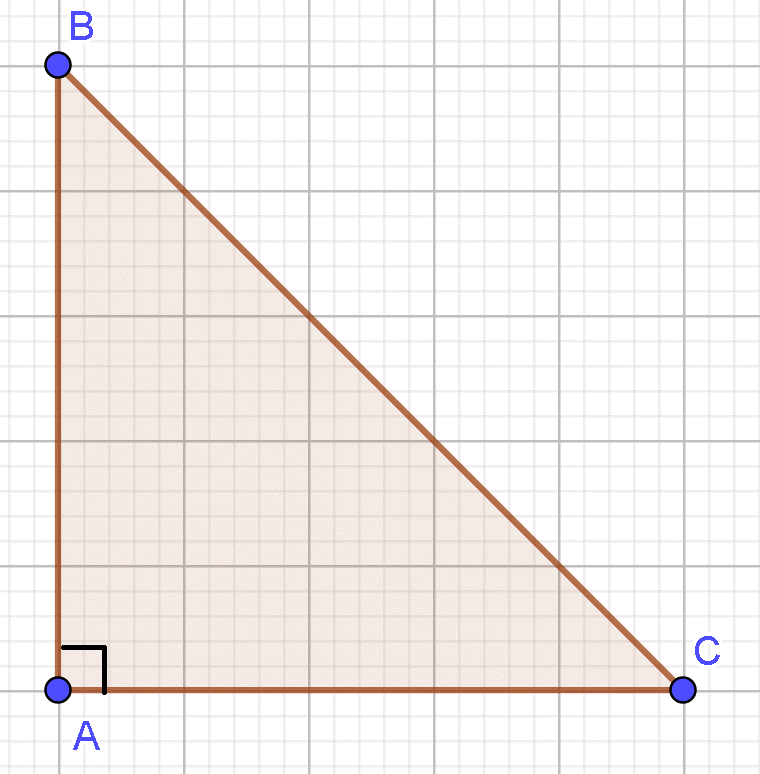
Áp dung định lý Py – ta – go ta có:

$A B^{2} + A C^{2} = B C^{2}$

$\Leftrightarrow B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{c^{2} + b^{2}}$

Cos B = $\frac{A B}{B C} = \frac{c}{\sqrt{b^{2} + c^{2}}}$

Lại có: cos B chính là cos $(\vec{B A}; \vec{B C})$

Ta có:

$\vec{B A} . \vec{B C} = B A . B C . c o s (\vec{B A}, \vec{B C}) = B A . B C . c o s \hat{B} = c . \sqrt{b^{2} + c^{2}} . \frac{c}{\sqrt{b^{2} + c^{2}}} = c^{2} .$

Câu 29:

Tam giác ABC có $B C = 2 \sqrt{3}, A C = 2 A B$ và độ dài đường cao AH = 2. Tính độ dài cạnh AB.

A. AB = 2;

B. $A B = \frac{2 \sqrt{3}}{3}$

C. AB = 2 hoặc

A B = \frac{2 \sqrt{21}}{3}

;

D. $A B = 2 h o ặ c A B = \frac{2 \sqrt{3}}{3};$

Xem đáp án

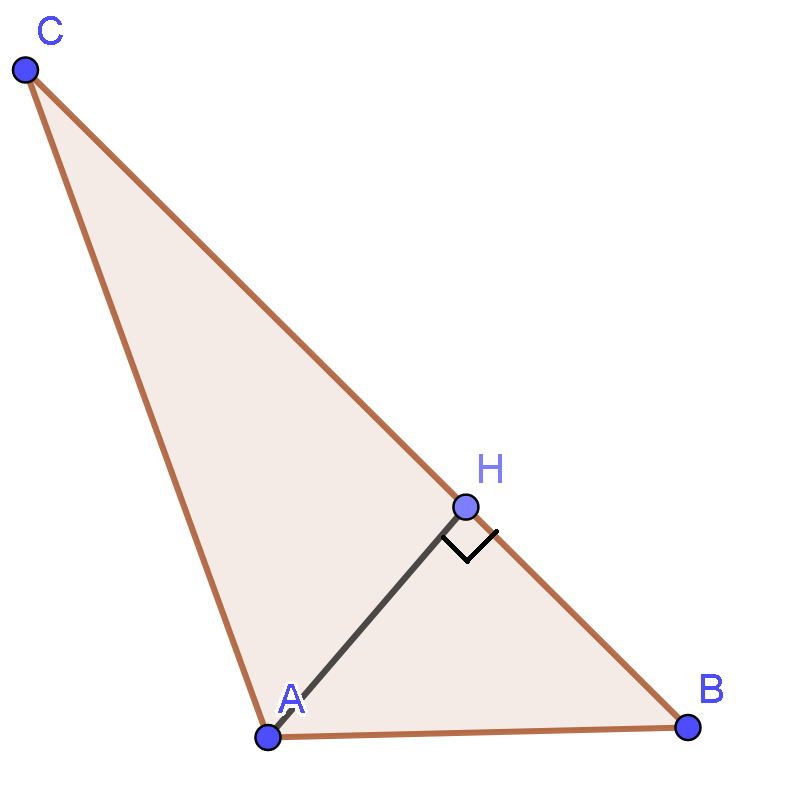
Đáp án đúng là: C

Nửa chu vi là:

Ta có: $p = \frac{A B + B C + C A}{2} = \frac{2 \sqrt{3} + 3 A B}{2}$ .

Suy ra $S = \sqrt{(\frac{3 A B + 2 \sqrt{3}}{2}) (\frac{3 A B - 2 \sqrt{3}}{2}) (\frac{2 \sqrt{3} - A B}{2}) (\frac{2 \sqrt{3} + A B}{2})}$ .

Lại có $S = \frac{1}{2} B C . A H = 2 \sqrt{3}$ (đơn vị diện tích).

Từ đó ta có: $2 \sqrt{3} = (\frac{3 A B + 2 \sqrt{3}}{2}) (\frac{3 A B - 2 \sqrt{3}}{2}) (\frac{2 \sqrt{3} - A B}{2}) (\frac{2 \sqrt{3} + A B}{2})$

$\Leftrightarrow 12 = \frac{(9 A B^{2} - 12) (12 - A B^{2})}{16} \Leftrightarrow [\begin{array}{l} A B = 2 \\ A B = \frac{2 \sqrt{21}}{3} \end{array} .$

Câu 30:

Cho tam giác ABC có $B C = a, C A = b, A B = c .$ Gọi M là trung điểm cạnh BC Tính $\vec{A M} . \vec{B C} .$

A. $\vec{A M} . \vec{B C} = \frac{b^{2} - c^{2}}{2};$

B. $\vec{A M} . \vec{B C} = \frac{c^{2} + b^{2}}{2};$

C. $\vec{A M} . \vec{B C} = \frac{c^{2} + b^{2} + a^{2}}{3};$

D. $\vec{A M} . \vec{B C} = \frac{c^{2} + b^{2} - a^{2}}{2} .$

Xem đáp án

Đáp án đúng là: A

Vì M là trung điểm của BC suy ra $\vec{A B} + \vec{A C} = 2 \vec{A M} .$

Khi đó $\vec{A M} . \vec{B C} = \frac{1}{2} (\vec{A B} + \vec{A C}) . \vec{B C} = \frac{1}{2} (\vec{A B} + \vec{A C}) . (\vec{B A} + \vec{A C})$

$= \frac{1}{2} (\vec{A C} + \vec{A B}) . (\vec{A C} - \vec{A B}) = \frac{1}{2} ({\vec{A C}}^{2} - {\vec{A B}}^{2}) = \frac{1}{2} (A C^{2} - A B^{2}) = \frac{b^{2} - c^{2}}{2} .$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Ôn tập chương 4 có đáp án

Trắc nghiệm Toán 10 Ôn tập chương 4 có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương