Cho tứ diện ABCD có AB = AC = AD và BAC^=BAD^=60°, CAD^=90°. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→ ?

Câu hỏi:

16/07/2024 209

Cho tứ diện ABCD có AB = AC = AD và $\hat{BAC} = \hat{BAD} = 60 °,$ $\hat{CAD} = 90 °$ . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ $\vec{AB}$ và $\vec{IJ}$ ?

A. 120°.

B. 90°.

Đáp án chính xác

C. 60°.

D. 45°.

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

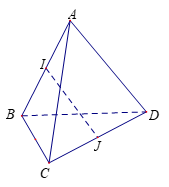
Xét tam giác ICD có J là trung điểm đoạn CD.

Ta có: $\vec{I J} = \frac{1}{2} (\vec{IC} + \vec{ID})$

Vì tam giác ABC có AB = AC và $\hat{BAC} = 60 °$

Nên tam giác ABC đều. Suy ra: $CI ⊥ AB$

Tương tự ta có tam giác ABD đều nên $DI ⊥ AB$ .

Xét $\vec{IJ} . \vec{AB} = \frac{1}{2} (\vec{IC} + \vec{ID}) . \vec{AB}$ $= \frac{1}{2} \vec{IC} . \vec{AB} + \frac{1}{2} \vec{ID} . \vec{AB}$ $= \vec{0}$

Suy ra $\vec{I J} ⊥ \vec{AB}$ . Hay góc giữa cặp vectơ $\vec{AB}$ và $\vec{IJ}$ bằng 90°.

Chọn đáp án B.

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 9}{x + 3} khi x \neq - 3 \\ - x^{2} + 3 khi x = - 3 \end{cases}$ . Khẳng định nào sau đây là đúng?

Xem đáp án » 01/07/2022 226

Câu 2:

Cho các dãy số (u_n), (v_n) và $\lim u_{n} = a,$ $\lim v_{n} = + \infty$ thì $\lim \frac{u_{n}}{v_{n}}$ bằng

Xem đáp án » 01/07/2022 192

Câu 3:

Biết $\lim \frac{2 n^{3} + n^{2} - 4}{2 + n + 4 n^{3}} = L$ . Khi đó 1 – L² bằng

Xem đáp án » 01/07/2022 180

Câu 4:

Cho hàm số: $f (x) = \{\begin{cases} \sqrt{\frac{x^{2} + 3}{x^{2} - 2 x - 3}} khi x \neq 4 \\ a + 5 khi x = 4 \end{cases}$ , tìm a để f(x) liên tục tại x = 4.

Xem đáp án » 01/07/2022 175

Câu 5:

Đặt lim u_n = a, lim v_n = b. Mệnh đề nào dưới đây sai?

Xem đáp án » 01/07/2022 175

Câu 6:

Cho $\lim_{x \to 1} f (x) = 3$ , $\lim_{x \to 1} g (x) = - 2$ . Tính $\lim_{x \to 1} [2 f (x) - 3 g (x)]$ ?

Xem đáp án » 01/07/2022 173

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết SA vuông góc với đáy và AB = SA = a, AC = 2a. Tính góc giữa hai đường thẳng SD và BC.

Xem đáp án » 01/07/2022 156

Câu 8:

Tính $\lim_{x \to - \infty} \frac{5 x - 3}{\sqrt{x^{2} - 5}}$

Xem đáp án » 01/07/2022 144

Câu 9:

Tính giới hạn $\lim (\frac{1}{3} + \frac{1}{6} + \frac{1}{10} + . .. + \frac{2}{(n + 1) (n + 2)}),$ $n \in ℕ^{*}$ .

Xem đáp án » 01/07/2022 140

Câu 10:

Cho dãy số (u_n) thỏa mãn lim(u_n – 2021) = 0. Giá trị của lim u_n bằng

Xem đáp án » 01/07/2022 140

Câu 11:

Kết quả của giới hạn $\lim_{x \to 0^{-}} \frac{|x|}{x}$ là

Xem đáp án » 01/07/2022 139

Câu 12:

Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB'. Đặt $\vec{CA} = \vec{a}, \vec{CB} = \vec{b},$ $\vec{AA'} = \vec{c}$ . Khẳng định nào sau đây đúng?

Xem đáp án » 01/07/2022 138

Câu 13:

Tìm a để $\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \frac{3}{4} .$

Xem đáp án » 01/07/2022 137

Câu 14:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 5 x + 6}{\sqrt{4 x + 1} - 3} khi x > 2 \\ 2 mx - 1 khi x \leq 2 \end{cases}$ . Tìm giá trị của tham số m để hàm số liên tục trên $ℝ$ .

Xem đáp án » 01/07/2022 137

Câu 15:

Cho tứ diện đều ABCD. Tích vô hướng $\vec{AB} . \vec{CD}$ bằng?

Xem đáp án » 01/07/2022 136

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản

7 đề 40133 lượt thi Thi thử
93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải

5 đề 29987 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn nâng cao

4 đề 24838 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn cơ bản

4 đề 24168 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao

6 đề 19772 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác cơ bản

5 đề 18701 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác nâng cao

6 đề 18500 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm cơ bản

6 đề 17739 lượt thi Thi thử
Trắc nghiệm Hàm số lượng giác có đáp án

2 đề 15912 lượt thi Thi thử
Bài tập Lượng Giác cơ bản , nâng cao có lời giải

13 đề 12475 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Cho hàm số $f (x) = {(3 x^{2} - 2 x - 1)}^{9}$ . Tính đạo hàm cấp 6 của hàm số tại điểm x=0.

322 21/10/2022 Xem đáp án
Cho hàm số $y = \sin \frac{x}{2}$ . Đạo hàm $y^{(n)}$ là

230 21/10/2022 Xem đáp án
Cho hàm số y=sin3x.cosx-sin2x . Giá trị của $y^{(10)} (\frac{π}{3})$ gần nhất với số nào dưới đây?

325 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=sin2x là

227 21/10/2022 Xem đáp án
Đạo hàm cấp 2021 của hàm số f(x)=cos(x+a) là

230 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{x}{x^{2} + 5 x + 6}$ là

235 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{2 x + 1}{x^{2} - 3 x + 2}$ là

283 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \sqrt{2 x + 1}$ là

290 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=cos2x là

357 21/10/2022 Xem đáp án
Cho hàm số $y = \sin^{2} 2 x$ . Giá trị của biểu thức $y^{(3)} + {y^{'}}^{'} + 16 y^{'} + 16 y - 8$ là

216 21/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Cho tứ diện ABCD có AB = AC = AD và BAC^=BAD^=60°, CAD^=90°. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→ ?

A. 120°.

B. 90°.

C. 60°.

D. 45°.

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hàm số f(x)=x2−9x+3 khi x≠−3−x2+3 khi x=−3. Khẳng định nào sau đây là đúng?

Câu 2:

Cho các dãy số (un), (vn) và lim un=a, lim vn=+∞ thì limunvn bằng

Câu 3:

Biết lim2n3+n2−42+n+4n3=L. Khi đó 1 – L2 bằng

Câu 4:

Cho hàm số: fx=x2+3x2−2x−3 khi x≠4a+5 khi x=4, tìm a để f(x) liên tục tại x = 4.

Câu 5:

Cho tứ diện ABCD có AB = AC = AD và $\hat{BAC} = \hat{BAD} = 60 °,$ $\hat{CAD} = 90 °$ . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ $\vec{AB}$ và $\vec{IJ}$ ?

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 9}{x + 3} khi x \neq - 3 \\ - x^{2} + 3 khi x = - 3 \end{cases}$ . Khẳng định nào sau đây là đúng?

Cho các dãy số (u_n), (v_n) và $\lim u_{n} = a,$ $\lim v_{n} = + \infty$ thì $\lim \frac{u_{n}}{v_{n}}$ bằng

Biết $\lim \frac{2 n^{3} + n^{2} - 4}{2 + n + 4 n^{3}} = L$ . Khi đó 1 – L² bằng

Cho hàm số: $f (x) = \{\begin{cases} \sqrt{\frac{x^{2} + 3}{x^{2} - 2 x - 3}} khi x \neq 4 \\ a + 5 khi x = 4 \end{cases}$ , tìm a để f(x) liên tục tại x = 4.