39 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 6)

Câu 1:

Cho dãy số (u_n) thỏa mãn lim(u_n – 2021) = 0. Giá trị của lim u_n bằng

A. +∞.

B. 0.

C. –2021.

D. 2021.

Xem đáp án

Áp dụng định nghĩa 2 trang 113 sách giáo khoa Đại số và Gải tích 11 ban Cơ bản ta có lim u_n = 2021.

Chọn đáp án D.

Câu 2:

Trong các giới hạn sau, giới hạn nào có giá trị bằng 1?

A. $\lim \frac{3 n + 1}{- 3 n - 3}$

B. $\lim \frac{1 - n}{n + 2}$

C. $\lim \frac{1 + n}{n - 1}$

D. $\lim (- 1 + \frac{2}{n})$

Xem đáp án

Vì $\lim \frac{3 n + 1}{- 3 n - 3} = \lim \frac{1 - n}{n + 2}$ $= \lim (- 1 + \frac{2}{n})$ $= - 1$

Còn $\lim \frac{1 + n}{n - 1} = 1$

Chọn đáp án C.

Câu 3:

Đặt lim u_n = a, lim v_n = b. Mệnh đề nào dưới đây sai?

A. $\lim (u_{n} . v_{n}) = \lim u_{n} + \lim v_{n} .$

B. $\lim (u_{n} + v_{n}) = \lim u_{n} + \lim v_{n} .$

C. $\lim (u_{n} - v_{n}) = \lim u_{n} - \lim v_{n} .$

D. $\lim (u_{n} . v_{n}) = \lim u_{n} . \lim v_{n} .$

Xem đáp án

Mệnh đề $\lim (u_{n} . v_{n}) = \lim u_{n} . \lim v_{n}$ là mệnh đề đúng nên mệnh đề ở câu A sai.

Chọn đáp án A.

Câu 4:

Chọn khẳng định đúng.

A. Dãy số (u_n) có giới hạn là –∞ khi n → +∞ nếu u_n lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

B. Dãy số (u_n) có giới hạn là +∞ khi n → +∞ nếu u_n nhỏ hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

C. Dãy số (u_n) có giới hạn là +∞ khi n → +∞ nếu u_n lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

D. Dãy số (u_n) có giới hạn là –∞ khi n → +∞ nếu u_n nhỏ hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

Xem đáp án

Dãy số (u_n) có giới hạn là +∞ khi n → +∞ nếu u_n lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi, do đó chọn C.

Chọn đáp án C.

Câu 5:

Trong các mệnh đề sau, mệnh đề nào sai?

A. lim qⁿ = +∞ (với |q| > 1).

B. Nếu lim u_n = a > 0, lim v_n = 0 và v_n > 0, thì $\lim \frac{u_{n}}{v_{n}} = + \infty$

C. $\lim n^{k} = + \infty$ với k là một số nguyên dương.

D. $\lim q^{n} = 0$ với $|q| < 1$ .

Xem đáp án

Mệnh đề A chỉ đúng với q thỏa mãn q > 1, với q < – 1 thì không tồn tại giới hạn dãy số qⁿ.

Mệnh đề B đúng theo định lí về giới hạn vô cực.

Mệnh đề C và D đúng theo kết quả của giới hạn đặc biệt.

Chọn đáp án A.

Câu 6:

Cho các dãy số (u_n), (v_n) và

\lim u_{n} = a,

\lim v_{n} = + \infty

thì

\lim \frac{u_{n}}{v_{n}}

bằng

A. 1.

B. 0.

C. –∞.

D. +∞.

Xem đáp án

Dùng định lý giới hạn: cho dãy số (u_n), (v_n) và $\lim u_{n} = a,$ ${limv}_{n} = + \infty$ trong đó a hữu hạn thì $\lim \frac{u_{n}}{v_{n}} = 0$

Chọn đáp án B.

Câu 7:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu

\lim |u_{n}| = + \infty

thì

\lim u_{n} = - \infty

B. Nếu $\lim u_{n} = - a$ thì $\lim |u_{n}| = a$

C. Nếu $\lim u_{n} = 0$ thì $\lim |u_{n}| = 0$ .

D. Nếu $\lim |u_{n}| = + \infty$ thì $\lim u_{n} = + \infty$

Xem đáp án

Nếu $\lim |u_{n}| = + \infty$ thì $\lim u_{n} = + \infty$ hoặc $\lim u_{n} = - \infty$

Nếu $\lim u_{n} = - a$ thì $\lim |u_{n}| = a$ thì a > 0.

Còn $\lim u_{n} = 0$ thì $\lim |u_{n}| = 0$ là mệnh đề đúng.

Chọn đáp án C.

Câu 8:

Cho $\lim_{x \to 2} f (x) = 0$ , $\lim_{x \to 2} g (x) = 2021$ . Tính $\lim_{x \to 2} \frac{f (x)}{g (x)}$ (nếu có).

A. +∞ .

B. Không tồn tại $\lim_{x \to 2} \frac{f (x)}{g (x)}$

C. –∞.

D. 0.

Xem đáp án

Ta có: $\lim_{x \to 2} \frac{f (x)}{g (x)} = \frac{0}{2021} = 0$

Chọn đáp án D.

Câu 9:

$\lim_{x \to + \infty} (x^{3} + 2 x^{2} - 1)$ bằng

A. 0.

B. 1.

C. +∞.

D. –∞.

Xem đáp án

Ta có: $\lim_{x \to + \infty} (x^{3} + 2 x^{2} - 1)$ $= \lim_{x \to + \infty} x^{3} (1 + \frac{2}{x} - \frac{1}{x^{3}})$

Vì $\lim_{x \to + \infty} x^{3} = + \infty$ và $\lim_{x \to + \infty} (1 + \frac{2}{x} - \frac{1}{x^{3}}) = 1 > 0$

Suy ra $\lim_{x \to + \infty} x^{3} (1 + \frac{2}{x} - \frac{1}{x^{3}}) = + \infty$

Vậy $\lim_{x \to + \infty} (x^{3} + 2 x^{2} - 1) = + \infty$

Chọn đáp án C.

Câu 10:

Cho $\lim_{x \to 1} f (x) = 3$ , $\lim_{x \to 1} g (x) = - 2$ . Tính $\lim_{x \to 1} [2 f (x) - 3 g (x)]$ ?

A. 0.

B. 5.

C. 12.

D. 13.

Xem đáp án

Có $\lim_{x \to 1} [2 f (x) - 3 g (x)]$ $\underset{x \to 1}{= \lim} 2 f (x) - \lim_{x \to 1} 3 g (x)$ $\underset{x \to 1}{= 2 \lim} f (x) - 3 \lim_{x \to 1} g (x)$ $= 2 .3 - 3 . (- 2) = 12$

Chọn đáp án C.

Câu 11:

Kết quả của giới hạn $\lim_{x \to 0^{-}} \frac{|x|}{x}$ là

A. 0.

B. 1.

C. –1.

D. +∞.

Xem đáp án

$\lim_{x \to 0^{-}} \frac{|x|}{x} = \lim_{x \to 0^{-}} \frac{- x}{x} = \lim_{x \to 0^{-}} (- 1)$ $= - 1$

Chọn đáp án C.

Câu 12:

Kết quả của giới hạn

\lim_{x \to - \infty} (- x^{4})

là

A. 0.

B. +∞.

C. –∞.

D. –1.

Xem đáp án

Ta có: $\lim_{x \to - \infty} (- x^{4})$ = –∞.

Chọn đáp án C.

Câu 13:

Kết quả của giới hạn

\lim_{x \to 2} (x^{2} - 2 x - 1)

là

A. –∞.

B. 0.

C. +∞.

D. –1.

Xem đáp án

$\lim_{x \to 2} (x^{2} - 2 x - 1) = 2^{2} - 2 .2 - 1$ $= - 1$

Chọn đáp án D.

Câu 14:

Hàm số nào sau đây không liên tục tại x = 0?

A. $f (x) = \frac{x^{2} + x + 1}{x - 1} .$

B. $f (x) = \frac{x^{2} + x + 1}{x} .$

C. $f (x) = \frac{x^{2} + x}{x + 2} .$

D. $f (x) = \frac{x^{2} + x}{x - 1} .$

Xem đáp án

Hàm số $f (x) = \frac{x^{2} + x + 1}{x}$ không xác định tại x = 0 nên hàm số không liên tục tại x = 0.

Chọn đáp án B.

Câu 15:

Khẳng định nào đúng ?

A. Hàm số $f (x) = \frac{x + 1}{\sqrt{x^{2} + 1}}$ xác định trên $ℝ .$

B. Hàm số $f (x) = \frac{x + 1}{x - 1}$ liên tục trên $ℝ$ .

C. Hàm số $f (x) = \frac{x + 1}{\sqrt{x - 1}}$ liên tục trên $ℝ$ .

D. Hàm số $f (x) = \frac{\sqrt{x + 1}}{x - 1}$ liên tục trên $ℝ$ .

Xem đáp án

Hàm số $f (x) = \frac{x + 1}{\sqrt{x^{2} + 1}}$ là hàm sơ cấp xác định trên $ℝ$ nên liên tục trên $ℝ$ .

Chọn đáp án A.

Câu 16:

Trong các mệnh đề sau mệnh đề nào sai?

A. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thảnh đoạn thẳng.

B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.

C. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi thứ tự của ba điểm đó.

D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

Xem đáp án

Tính chất của phép chiếu song song:

Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

Suy ra B sai : Chúng có thể trùng nhau.

Chọn đáp án B.

Câu 17:

Cho ba vectơ

\vec{a}, \vec{b}, \vec{c}

. Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.

A. Một trong ba vecto đó bằng $\vec{0} .$

B. Có hai trong ba vecto đó cùng phương.

C. Có một vecto không cùng hướng với hai vecto còn lại.

D. Có hai trong ba vecto đó cùng hướng.

Xem đáp án

Nếu hai trong ba vectơ đó cùng hướng thì ba vectơ đồng phẳng; nếu hai trong ba vectơ đó không cùng hướng thì chưa thể kết luận được ba vectơ đó đồng phẳng.

Chọn đáp án C.

Câu 18:

Cho hình hộp ABCD.A'B'C'D', M, N là các điểm thỏa mãn

\vec{MA} = - \frac{1}{4} \vec{MD}

,

\vec{NA'} = - \frac{2}{3} \vec{NC}

. Mệnh đề nào sau đây đúng?

A.

MN // (AC' B)

.

B. $MN // (BC' D) .$

C. $MN // (A' C' D) .$

D. $MN // (BC' B) .$

Xem đáp án

Nếu hai trong ba vectơ đó cùng hướng thì ba vectơ đồng phẳng; nếu hai trong ba vectơ đó không cùng hướng thì chưa thể kết luận được ba vectơ đó đồng phẳng. Chọn đáp án C. (ảnh 1)

Đặt $\vec{BA} = \vec{a}, \vec{BB'} = \vec{b}, \vec{BC} = \vec{c}$ thì $\vec{a}, \vec{b}, \vec{c}$ là ba vec tơ không đồng phẳng và $\vec{BD} = \vec{BA} + \vec{AD} = \vec{BA} + \vec{BC} = \vec{a} + \vec{c};$ $\vec{BC'} = \vec{b} + \vec{c}, \vec{BA'} = \vec{a} + \vec{b}$

Ta có $\vec{MA} = - \frac{1}{4} \vec{MD}$ $\Rightarrow \vec{BA} - \vec{BM} = - \frac{1}{4} (\vec{BD} - \vec{BM})$ $\Rightarrow \frac{5}{4} \vec{BM} = \vec{BA} + \frac{1}{4} \vec{BD}$

$\Rightarrow \vec{BM} = \frac{4 \vec{BA} + \vec{BD}}{5} = \frac{4 \vec{a} + (\vec{a} + \vec{c})}{5}$ $= \frac{5 \vec{a} + \vec{c}}{5}$

Tương tự $\vec{BN} = \frac{3 \vec{a} + 3 \vec{b} + 2 \vec{c}}{5}$

$\vec{MN} = \vec{BN} - \vec{BM} = \frac{- 2 \vec{a} + 3 \vec{b} + \vec{c}}{5}$ $= - \frac{2}{5} (\vec{a} + \vec{c}) + \frac{3}{5} (\vec{b} + \vec{c})$ $= - \frac{2}{5} \vec{BD} + \frac{3}{5} \vec{BC'}$

Suy ra $\vec{MN}, \vec{DB}, \vec{BC'}$ đồng phẳng mà $N \notin (BC' D)$ $\Rightarrow MN // (BC' D)$

Chọn đáp án B.

Câu 19:

Cho tứ diện đều ABCD. Tích vô hướng

\vec{AB} . \vec{CD}

bằng?

A. a².

B.

\frac{a^{2}}{2}

.

C. 0.

D. $- \frac{a^{2}}{2}$ .

Xem đáp án

Cho tứ diện đều ABCD. Tích vô hướng AB→.CD→ bằng? (ảnh 1)

$\vec{AB} . \vec{CD} = (\vec{CB} - \vec{CA}) . \vec{CD}$ $= CB . CD . \cos 60^{0} - CA . CD . \cos 60^{0}$ $= 0$ .

Chọn đáp án C.

Câu 20:

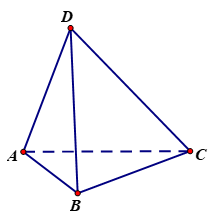
Cho tứ diện ABCD có AB = AC = AD và $\hat{BAC} = \hat{BAD} = 60 °$ . Hãy xác định góc giữa cặp vectơ $\vec{AB}$ và $\vec{CD}$ .

A. 60°.

B. 45°.

C. 120°.

D. 90°.

Xem đáp án

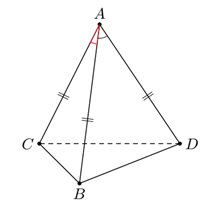
Cho tứ diện ABCD có AB = AC = AD và BAC^=BAD^=60° . Hãy xác định góc giữa cặp vectơ AB→ và CD→ . (ảnh 1)

\vec{AB} . \vec{CD} = \vec{AB} . (\vec{AD} - \vec{AC})

= \vec{AB} . \vec{AD} - \vec{AB} . \vec{AC}

= |\vec{AB}| . |\vec{AD}| \cos (\vec{AB}, \vec{AD}) -

|\vec{AB}| . |\vec{AC}| \cos (\vec{AB}, \vec{AC})

= |\vec{AB}| . |\vec{AD}| \cos 60^{0} -

|\vec{AB}| . |\vec{AC}| \cos 60^{0}

Mà

AC = AD \Rightarrow \vec{AB} . \vec{CD} = 0

\Rightarrow (\vec{AB}, \vec{CD}) = 90^{0}

Chọn đáp án D.

Câu 21:

Tìm a để

\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \frac{3}{4} .

A. a = 6.

B. a = 3.

C. a = 27.

D. a = 9.

Xem đáp án

$\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \lim \frac{a + \frac{4}{n}}{8 + \frac{3}{n^{2}}}$ $= \frac{\lim (a + \frac{4}{n})}{\lim (8 + \frac{3}{n^{2}})}$ $= \frac{a}{8} .$

$\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \frac{3}{4} \Leftrightarrow \frac{a}{8} = \frac{3}{4}$ $\Leftrightarrow a = 6 .$

Chọn đáp án A.

Câu 22:

Tính tổng $S = 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + . .. + \frac{1}{{(- 2)}^{n - 1}} + . ..$

A. $S = \frac{3}{2}$

B. $S = \frac{2}{3}$

C.

S = 2

D. $S = \frac{1}{2}$

Xem đáp án

S là tổng của cấp số nhân lùi vô hạn với $u_{1} = 1;$ $q = - \frac{1}{2}$

Do đó ta có: $S = \frac{u_{1}}{1 - q} = \frac{1}{1 - (- \frac{1}{2})} = \frac{2}{3}$

Chọn đáp án B.

Câu 23:

Biết $\lim \frac{2 n^{3} + n^{2} - 4}{2 + n + 4 n^{3}} = L$ . Khi đó 1 – L² bằng

A. 1.

B. $\frac{3}{4} .$

C. 0.

D. $\frac{1}{4} .$

Xem đáp án

$\lim \frac{2 n^{3} + n^{2} - 4}{2 + n + 4 n^{3}} = \lim \frac{n^{3} (2 + \frac{1}{n} - \frac{4}{n^{3}})}{n^{3} (\frac{2}{n^{3}} + \frac{1}{n^{2}} + 4)}$ $= \frac{2}{4} = \frac{1}{2}$

Suy ra $L = \frac{1}{2}$ . Khi đó $1 - L^{2} = 1 - {(\frac{1}{2})}^{2} = \frac{3}{4}$

Chọn đáp án B.

Câu 24:

Tính $\lim_{x \to - \infty} \frac{5 x - 3}{\sqrt{x^{2} - 5}}$

A. $\frac{3}{5} .$

B. $- \frac{3}{5} .$

C. 5.

D. –5.

Xem đáp án

$\lim_{x \to - \infty} \frac{5 x - 3}{\sqrt{x^{2} - 5}} = \lim_{x \to - \infty} \frac{x (5 - \frac{3}{x})}{|x| \sqrt{1 - \frac{5}{x^{2}}}} = \lim_{x \to - \infty} \frac{x (5 - \frac{3}{x})}{- x \sqrt{1 - \frac{5}{x^{2}}}} = \lim_{x \to - \infty} \frac{5 - \frac{3}{x}}{- \sqrt{1 - \frac{5}{x^{2}}}} = - 5$

Chọn đáp án D.

Câu 25:

Tính

\lim_{x \to 0^{+}} \frac{2 x + 1}{x}

bằng

A. 2.

B.

- \infty

.

C. $+ \infty .$

D. 1.

Xem đáp án

Vì $\lim_{x \to 0^{+}} (2 x + 1) = 1$ ; x>0 nên $\lim_{x \to 0^{+}} \frac{2 x + 1}{x} = + \infty$

Chọn đáp án C.

Câu 26:

Cho

\lim_{x \to - \infty} (\sqrt{x^{2} + ax + 5} + x) = 5

. Giá trị của a bằng bao nhiêu ?

A. 6.

B. 10.

C. –10.

D. –6.

Xem đáp án

$\lim_{x \to - \infty} (\sqrt{x^{2} + ax + 5} + x)$ $= \lim_{x \to - \infty} \frac{a . x + 5}{\sqrt{x^{2} + ax + 5} - x}$ $= - \frac{a}{2}$

Mà $\lim_{x \to - \infty} (\sqrt{x^{2} + ax + 5} + x) = 5$ $\Rightarrow - \frac{a}{2} = 5$ $\Leftrightarrow a = - 10$

Câu 27:

Cho hàm số

f (x) = \{\begin{cases} \frac{x^{2} - 9}{x + 3} khi x \neq - 3 \\ - x^{2} + 3 khi x = - 3 \end{cases}

. Khẳng định nào sau đây là đúng?

A. Hàm số chỉ liên tục tại điểm x = –3 và gián đoạn tại các điểm x ≠ –3.

B. Hàm số không liên tục trên $ℝ$ .

C. Hàm số liên tục trên $ℝ$ .

D. Hàm số không liên tục tại điểm x = –3.

Xem đáp án

+ Với x ≠ – 3: $f (x) = \frac{x^{2} - 9}{x + 3}$ .

Đây là hàm phân thức hữu tỉ nên hàm số liên tục trên $(- \infty; - 3), (- 3; + \infty)$ .

+ Tại x = –3: $f (- 3) = - 6$ ; $\lim_{x \to - 3} \frac{x^{2} - 9}{x + 3} = \lim_{x \to - 3} \frac{(x - 3) (x + 3)}{x + 3}$ $= \lim_{x \to - 3} (x - 3)$ $= - 6$

Vậy hàm số đã cho liên tục tại x = –3.

Vậy hàm số liên tục trên $ℝ$ .

Chọn đáp án C.

Câu 28:

Cho hàm số:

f (x) = \{\begin{cases} \sqrt{\frac{x^{2} + 3}{x^{2} - 2 x - 3}} khi x \neq 4 \\ a + 5 khi x = 4 \end{cases}

, tìm a để f(x) liên tục tại x = 4.

A. $a = \sqrt{\frac{19}{5}} + 5$

B. $a = \sqrt{\frac{19}{5}} - 5$

C. a = –5.

D. a = 5.

Xem đáp án

Ta có f(x) liên tục tại x = 4 thì:

$\lim_{x \to 4} f (x) = \lim_{x \to 4} \sqrt{\frac{x^{2} + 3}{x^{2} - 2 x - 3}}$ $= \sqrt{\frac{4^{2} + 3}{4^{2} - 2 .4 - 3}}$ $= \sqrt{\frac{19}{5}}$ $= f (4)$

$\Leftrightarrow a + 5 = f (4) = \sqrt{\frac{19}{5}}$ $\Leftrightarrow a = \sqrt{\frac{19}{5}} - 5$

Vậy $a = \sqrt{\frac{19}{5}} - 5$ thì hàm số liên tục tại x = 4.

Chọn đáp án B.

Câu 29:

Cho hàm số

f (x) = \{\begin{cases} \frac{x^{2} - 5 x + 6}{\sqrt{4 x + 1} - 3} khi x > 2 \\ 2 mx - 1 khi x \leq 2 \end{cases}

. Tìm giá trị của tham số m để hàm số liên tục trên

ℝ

.

A. $m = \frac{- 3}{2} .$

B. $m = \frac{- 1}{8} .$

C. $m = \frac{1}{8}$ .

D. $m = \frac{3}{2} .$

Xem đáp án

Tập xác định $D = ℝ$ .

Khi $x \in (2; + \infty)$ thì $f (x) = \frac{x^{2} - 5 x + 6}{\sqrt{4 x + 1} - 3}$ là hàm sơ cấp xác định trên $(2; + \infty)$ nên hàm số f(x) liên tục trên $(2; + \infty)$

Khi $x \in (- \infty; 2)$ thì $f (x) = 2 mx - 1$ là hàm đa thức nên hàm số liên tục trên $(- \infty; 2)$

Do đó hàm số liên tục trên $ℝ$ khi và chỉ khi hàm số liên tục tại x = 2.

Ta có: f(2) = 4m – 1.

$\lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{+}} \frac{x^{2} - 5 x + 6}{\sqrt{4 x + 1} - 3}$ $= \lim_{x \to 2^{+}} \frac{(x - 2) (x - 3) (\sqrt{4 x + 1} + 3)}{(4 x + 1 - 9)}$

$= \lim_{x \to 2^{+}} \frac{(x - 3) (\sqrt{4 x + 1} + 3)}{4}$ $= \frac{- 3}{2}$

$\lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{-}} (2 mx - 1) = 4 m - 1$

Hàm số liên tục tại x = 2 khi và chỉ khi:

$f (2) = \lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{-}} f (x)$ $\Leftrightarrow 4 m - 1 = \frac{- 3}{2}$ $\Leftrightarrow m = \frac{- 1}{8}$

Chọn đáp án B.

Câu 30:

Hàm số nào sau đây không liên tục trên

ℝ

?

A. $y = \sqrt{2 x^{2} + 1} .$

B. $y = \frac{2 x - 1}{x + 1} .$

C. $y = 4 x^{3} - 3 x + 1 .$

D. $y = \frac{2 x - 5}{x^{2} + 2} .$

Xem đáp án

Hàm số $y = \frac{2 x - 1}{x + 1}$ có tập xác định là $D = ℝ \ \{- 1\}$ nên hàm số bị gián đoạn tại điểm x = –1. Do đó hàm số $y = \frac{2 x - 1}{x + 1}$ không liên tục trên $ℝ$

Chọn đáp án B.

Câu 31:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết SA vuông góc với đáy và AB = SA = a, AC = 2a. Tính góc giữa hai đường thẳng SD và BC.

A. 30°.

B. 60°.

C. 90°.

D. 45°.

Xem đáp án

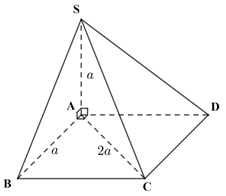
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết SA vuông góc với đáy và AB = SA = a, AC = 2a. Tính góc giữa hai đường thẳng SD và BC. (ảnh 1)

Tam giác ABC vuông tại B $\Rightarrow AD = BC = \sqrt{{AC}^{2} - {AB}^{2}}$ $= \sqrt{{(2 a)}^{2} - a^{2}}$ $= a \sqrt{3}$

Ta có BC // AD nên $\hat{(SD, BC)} = \hat{(SD, AD)} = \hat{SDA}$

Xét tam giác SAD vuông tại A, ta có $\tan \hat{SDA} = \frac{SA}{AD} = \frac{\sqrt{3}}{3} \Rightarrow \hat{SDA} = 30 °$

Vậy $\hat{(SD, BC)} = 30^{0}$ .

Chọn đáp án A.

Câu 32:

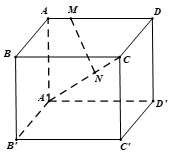
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ).

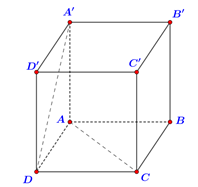
Góc giữa hai đường thẳng AC và A'D bằng

A. 45°.

B. 60°.

C. 30°.

D. 90°.

Xem đáp án

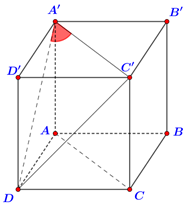
Do A'C' // AC nên ta có: $(AC, A^{'} D) = (A^{'} C^{'}, A^{'} D) = \hat{{DA}^{'} C^{'}}$ .

Vì $A^{'} D = A^{'} C^{'} = C^{'} D$ $\Rightarrow {ΔA}^{'} C^{'} D$ đều $\Rightarrow \hat{{DA}^{'} C^{'}} = 60 °$

Chọn đáp án B.

Câu 33:

Cho tứ diện ABCD có AB = AC = AD và

\hat{BAC} = \hat{BAD} = 60 °,

\hat{CAD} = 90 °

. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ

\vec{AB}

và

\vec{IJ}

?

A. 120°.

B. 90°.

C. 60°.

D. 45°.

Xem đáp án

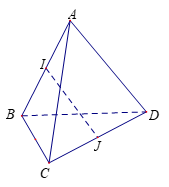
Cho tứ diện ABCD có AB = AC = AD và BAC^=BAD^=60°, CAD^=90° . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→ ? (ảnh 1)

Xét tam giác ICD có J là trung điểm đoạn CD.

Ta có: $\vec{I J} = \frac{1}{2} (\vec{IC} + \vec{ID})$

Vì tam giác ABC có AB = AC và $\hat{BAC} = 60 °$

Nên tam giác ABC đều. Suy ra: $CI ⊥ AB$

Tương tự ta có tam giác ABD đều nên $DI ⊥ AB$ .

Xét $\vec{IJ} . \vec{AB} = \frac{1}{2} (\vec{IC} + \vec{ID}) . \vec{AB}$ $= \frac{1}{2} \vec{IC} . \vec{AB} + \frac{1}{2} \vec{ID} . \vec{AB}$ $= \vec{0}$

Suy ra $\vec{I J} ⊥ \vec{AB}$ . Hay góc giữa cặp vectơ $\vec{AB}$ và $\vec{IJ}$ bằng 90°.

Chọn đáp án B.

Câu 34:

Trong không gian, cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây đúng?

A. Các vectơ $\vec{AB} + \vec{AD} + \vec{{AA}^{'}},$ $\vec{AB} + \vec{AD},$ $\vec{CB} - \vec{CA}$ đồng phẳng.

B. Các vectơ $\vec{{AA}^{'}}, \vec{{BB}^{'}}, \vec{{CC}^{'}}$ không đồng phẳng.

C. Các vectơ $\vec{AB} + \vec{AD},$ $\vec{C^{'} B^{'}} + \vec{C^{'} D^{'}},$ $\vec{A^{'} C}$ không đồng phẳng.

D. Các vectơ $\vec{{AB}^{'}} + \vec{{AD}^{'}},$ $\vec{AB} + \vec{{AA}^{'}},$ $\vec{AD} + \vec{{AA}^{'}}$ đồng phẳng.

Xem đáp án

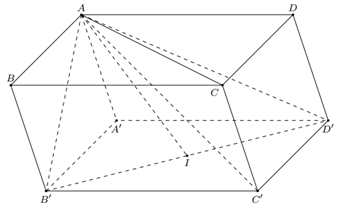
Trong không gian, cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây đúng? (ảnh 1)

Xét phương án A.

Ta có $\vec{AB} + \vec{AD} + \vec{{AA}^{'}} = \vec{{AC}^{'}}$ , $\vec{AB} + \vec{AD} = \vec{AC}$ , $\vec{CB} - \vec{CA} = \vec{AB}$ .

Các vectơ $\vec{AB}, \vec{AC}, \vec{{AC}^{'}}$ không đồng phẳng vì ABCC' là tứ diện.

Xét phương án B. Ta có $\vec{{AA}^{'}}, \vec{{BB}^{'}}, \vec{{CC}^{'}}$ đồng phẳng vì giá của chúng là các đường thẳng song song nhau nên sẽ luôn song song với một mặt phẳng nào đó.

Xét phương án C. Ta có $\vec{AB} + \vec{AD} = \vec{AC}, \vec{C^{'} B^{'}} + \vec{C^{'} D^{'}} = \vec{C^{'} A^{'}}$ . Các vectơ $\vec{AC}, \vec{C^{'} A^{'}}, \vec{A^{'} C}$ có giá là các đường thẳng cùng nằm trên mặt phẳng $({AA}^{'} C^{'} C)$ nên chúng đồng phẳng.

Xét phương án D. Ta có $\vec{AB} + \vec{{AA}^{'}} = \vec{{AB}^{'}}$ , $\vec{AD} + \vec{{AA}^{'}} = {AD}^{'}$ . Các vectơ $\vec{{AB}^{'}}, \vec{{AD}^{'}}, \vec{x} = \vec{{AB}^{'}} + \vec{{AD}^{'}}$ hiển nhiên đồng phẳng.

Chọn đáp án D.

Câu 35:

Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB'. Đặt

\vec{CA} = \vec{a}, \vec{CB} = \vec{b},

\vec{AA'} = \vec{c}

. Khẳng định nào sau đây đúng?

A. $\vec{AM} = \vec{a} - \vec{c} + \frac{1}{2} \vec{b}$

B. $AM = \vec{b} + \vec{c} - \frac{1}{2} \vec{a}$

C. $\vec{AM} = \vec{a} + \vec{c} - \frac{1}{2} \vec{b}$

D. $\vec{AM} = \vec{b} - \vec{a} + \frac{1}{2} \vec{c}$

Xem đáp án

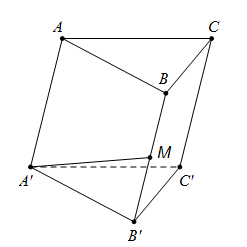
Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB'. Đặt CA→=a→,CB→=b→,AA'→=c→ . Khẳng định nào sau đây đúng? (ảnh 1)

Ta có: $\vec{AM} = \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{{AB}^{'}}$ $= \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{{AA}^{'}}$

$= \vec{AC} + \vec{CB} + \frac{1}{2} \vec{{AA}^{'}}$ $= \vec{b} - \vec{a} + \frac{1}{2} \vec{c}$ .

Chọn đáp án D.

Câu 36:

Tính giới hạn

\lim (\frac{1}{3} + \frac{1}{6} + \frac{1}{10} + . .. + \frac{2}{(n + 1) (n + 2)}),

n \in ℕ^{*}

.

Xem đáp án

$\lim (\frac{1}{3} + \frac{1}{6} + \frac{1}{10} + . .. + \frac{2}{(n + 1) (n + 2)}) = \lim [2 (\frac{1}{6} + \frac{1}{12} + \frac{1}{20} + . .. + \frac{1}{(n + 1) (n + 2)})] = \lim [2 . (\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + . .. + \frac{1}{n + 1} - \frac{1}{n + 2})] = \lim [2 . (\frac{1}{2} - \frac{1}{n + 2})] = 1$

Câu 37:

Cho hình hộp ABCD.EFGH. Gọi I là tâm của hình bình hành ABFE và K là tâm của hình bình hành BCGF. Chứng minh các vectơ

\vec{BD}, \vec{IK}, \vec{GF}

đồng phẳng.

Xem đáp án

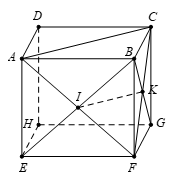
Vì I, K lần lượt là trung điểm của AF và CF.

Suy ra IK là đường trung bình của tam giác AFC ⇒ IK //AC ⇒ IK // (ABCD)

Mà GF // (ABCD) và BD ⊂ (ABCD) suy ra ba vectơ $\vec{BD}, \vec{IK}, \vec{GF}$ đồng phẳng.

Câu 38:

Một mô hình gồm các khối cầu xếp chồng lên nhau tạo thành một cột thẳng đứng. Biết rằng mỗi khối cầu có bán kính gấp đôi khối cầu nằm ngay trên nó và bán kính khối cầu dưới là 50 cm. Hỏi chiều cao tối đa của mô hình là bao nhiêu?

Xem đáp án

Gọi bán kính khối cầu dưới cùng là R = 50 cm.

Gọi $R_{1}, R_{2}, ..., R_{n}$ là các khối cầu nằm ngay trên khối cầu cuối cùng.

Ta có: $R_{2} = \frac{R_{1}}{2}, R_{3} = \frac{R_{2}}{2} = \frac{R_{1}}{4},$ $..., R_{n} = \frac{R_{n - 1}}{2} = \frac{R_{1}}{2^{n - 1}}$

Gọi h_n là chiều cao của mô hình gồm các khối cầu chồng lên nhau. Ta có $h_{n} = 2 R_{1} + 2 R_{2} + . .. + 2 R_{n}$

$= 2 (R_{1} + \frac{1}{2} R_{1} + \frac{1}{4} R_{1} + . .. + \frac{1}{2^{n - 1}} R_{1})$

$= 2 R_{1} (1 + \frac{1}{2} + \frac{1}{4} + . .. + \frac{1}{2^{n - 1}})$

$h = \lim_{n \to + \infty} h_{n} =$ $\lim_{n \to + \infty} [2 R_{1} (1 + \frac{1}{2} + \frac{1}{4} + . .. + \frac{1}{2^{n - 1}})]$

$= 2 R_{1} \frac{1}{1 - \frac{1}{2}} = 4 R_{1}$

Suy ra h = 4.50 = 200 cm = 2 m. Vậy chiều cao tối đa của mô hình là 2 m.

Câu 39:

Chứng minh rằng phương trình (m² + 1)x³ – 2m²x² – 4x + m² + 1 = 0 luôn có 3 nghiệm.

Xem đáp án

Đặt f(x) = (m² + 1)x³ – 2m²x² – 4x + m² + 1.

+ Hàm số f(x) = (m² + 1)x³ – 2m²x² – 4x + m² + 1 liên tục trên $ℝ$ .

+ Ta có: f(x) = m²(x³ – 2x² + 1) + x³ – 4x + 1

$f (- 3) = - 44 m^{2} - 14 < 0; \forall m$

$f (0) = m^{2} + 1 > 0, \forall m$

f(1) = – 2

$f (2) = m^{2} + 1 > 0; \forall m$

Vì f(– 3).f(0) < 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng (–3; 0).

Vì f(0).f(1) < 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng (0; 1).

Vì f(1).f(2) < 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng (1; 2).

Vậy phương trình có ít nhất 3 nghiệm trong khoảng (–3; 2), mà phương trình đã cho là bậc 3 nên phương trình có đúng 3 nghiệm.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 6)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương