Chứng minh rằng các đường cao của hình thoi bằng nhau.
Giải bởi qa.haylamdo.com
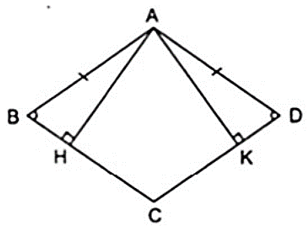
Xét hình thoi ABCD, kẻ hai đường cao
AH ⊥ BC, AK ⊥ CD.
Ta cần chứng minh: AH = AK.
Áp dụng định nghĩa, tính chất về góc và giả thiết của hình thoi ABCD, ta có:
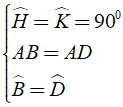
⇒ Δ ABH = Δ ADH ( g - c - g )
⇒ AH = AK (cặp cạnh tương ứng bằng nhau)
→ (đpcm)
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
Cho hình thang vuông ABCD có = 900 và CD = 2AB. Kẻ DE ⊥ AC, gọi I là trung điểm của EC. Chứng minh rằng = 900.
Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng:
a) AM = AN
