Với x thuộc tập hợp nào dưới đây thì f(x) = 2x2 – 7x – 15 không âm?
A. (−∞;−32]∪[5;+∞);
B. (−∞;−5]∪[32;+∞);
C. [−5;32];
D. [−32;5].
Giải bởi qa.haylamdo.com
Đáp án đúng là: A
Xét f(x) = 2x2 – 7x – 15 có ∆ = 169 > 0, hai nghiệm phân biệt là x = 5; x = −32 và a = 2 > 0
Ta có bảng xét dấu
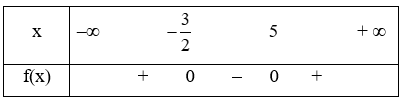
Từ bảng xét dấu ta có f(x) không âm khi x ∈ (−∞;−32]∪[5;+∞).
Có bao nhiêu giá trị nguyên của m để bất phương trình x2 + 3mx2 + 4mx + 4 ≥ 0 với mọi x ∈ ℝ.
Gọi x là nghiệm của phương trình
√3x−2+√x−1=4x−9+2√3x2−5x+2
Tính giá trị của biểu thức A = x2 – 3x + 15
Cho f(x) = x2 – 4. Tìm khẳng định sai trong các khẳng định sau đây
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi:
Nghiệm của phương trình √x−2+√x+3=5 thuộc khoảng nào trong các khoảng sau
Xác định m để bất phương trình x2 + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x ∈ ℝ.
