Tập nghiệm của bất phương trình x2 – 3x + 2 < 0 là:
A. (1; 2);
B. (–∞; 1) ∪ (2; +∞);
C. (–∞; 1);
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: A
Tam thức bậc hai f(x) = x2 – 3x + 2 có ∆ = (–3)2 – 4.1.2 = 1 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
Ta lại có a = 1 > 0.
Do đó ta có:
⦁ f(x) âm trên khoảng (1; 2);
⦁ f(x) dương trên hai khoảng (–∞; 1) và (2; +∞);
⦁ f(x) = 0 khi x = 1 hoặc x = 2.
Vì vậy bất phương trình x2 – 3x + 2 < 0 có tập nghiệm là (1; 2).
Ta chọn phương án A.
Cho bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0. Để x = 6 là một nghiệm của bất phương trình trên thì m nhận giá trị nào trong các giá trị sau đây?
Cho hàm số bậc hai f(x) có đồ thị như hình bên.
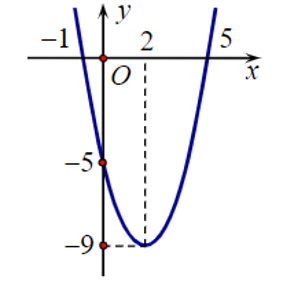
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
