Cho bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0. Để x = 6 là một nghiệm của bất phương trình trên thì m nhận giá trị nào trong các giá trị sau đây?
A. ;
B. ;
C. ;
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: A
Vì x = 6 là một nghiệm của bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0 nên ta có:
(m – 2).62 + 2(2m – 3).6 + 5m – 6 ≥ 0.
⇔ 36(m – 2) + 12(2m – 3) + 5m – 6 ≥ 0
⇔ 65m – 114 ≥ 0
Vậy thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Cho hàm số bậc hai f(x) có đồ thị như hình bên.
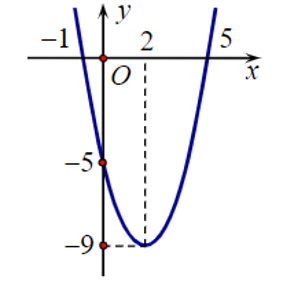
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
