Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tâm O, cạnh BC = a, SA = SB = SC = SD = 2a . Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA.
a) Chứng minh: SO ^ (ABCD).
b) Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
a)
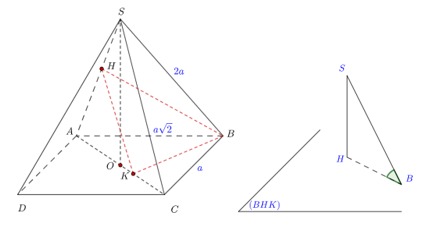
+ Xét tam giác SAC có SA = SC = 2a nên tam giác SAC cân tại S, có O là trung điểm của AC nên SO là đường trung tuyến và cũng là đường cao của tam giác SAC
Suy ra SO ^ AC (1)
+ Xét tam giác SAC có SB = SD = 2a nên tam giác SBD cân tại S, có O là trung điểm của BD nên SO là đường trung tuyến và cũng là đường cao của tam giác SBD
Suy ra SO ^ BD (2)
Từ (1) và (2) nên ta có SO ^ (ABCD)
b) Ta có:
Từ đó suy ra BK ^ SH
Mà KH ^ SH
Nên ta có SH ^ (BKH) Þ (SB, (BKH)) = (SB, HB) = a
Ta cũng suy ra được SH ^ BH
Ta có:
Cho hai dãy số (un), (vn) thỏa mãn lim un = 4 và lim vn = 2. Giá trị của lim (un.vn) bằng:
Trong không gian, cho tứ diện ABCD có các tam giác ABC cân tại A, tam giác DBC cân tại D. Gọi M trung điểm BC, khi đó BC lần lượt vuông góc với các cạnh AM và
DM. Khẳng định đúng là BC vuông góc với mặt phẳng nào dưới đây?Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đẳng thức nào đúng?
Cho hình chóp S.ABCD đáy là hình vuông cạnh a, tâm O. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi a là góc tạo bởi đường thẳng SC và mặt phẳng đáy.
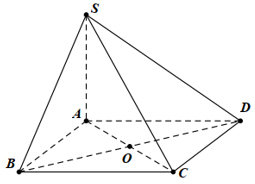
Mệnh đề nào sau đây đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai?