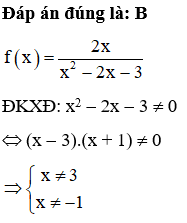38 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 7)

Câu 1:

Cho hai dãy số (u_n), (v_n) thỏa mãn lim u_n = 4 và lim v_n = 2. Giá trị của lim (u_n.v_n) bằng:

A. -2;

B. 6;

C. 2;

D. 8.

Xem đáp án

Đáp án đúng là: D

lim (u_n.v_n) = lim u_n.lim v_n = 4.2 = 8.

Câu 2:

$\lim {(\frac{4}{3})}^{n}$ bằng:

A. 2

B. 0

C. 1

D.+¥.

Xem đáp án

Đáp án đúng là: D

$\lim {(\frac{4}{3})}^{n} = + \infty$ (vì $\frac{4}{3} > 1$ ).

Câu 3:

Dãy số nào sau đây có giới hạn khác 0?

A. ${(\frac{4}{3})}^{n};$

B. $\frac{1}{\sqrt{n}};$

C. $\frac{{(- 1)}^{n}}{n};$

D. $\frac{1}{2 n} .$

Xem đáp án

Đáp án đúng là: A

$\lim {(\frac{4}{3})}^{n} = + \infty$ ;

$\lim \frac{1}{\sqrt{n}} = 0$ ;

$\lim \frac{{(- 1)}^{n}}{n} = 0$ ;

$\lim \frac{1}{2 n} = 0.$

Câu 4:

$\lim_{x \to 1} \frac{2 x + 1}{2 x - 1}$ bằng:

A. 5

B. +¥

C. 3;

D. -¥.

Xem đáp án

Đáp án đúng là: C

$\lim_{x \to 1} \frac{2 x + 1}{2 x - 1} = \frac{2.1 + 1}{2.1 - 1} = 3.$

Câu 5:

Trong không gian, cho tứ diện ABCD có các tam giác ABC cân tại A, tam giác DBC cân tại D. Gọi M trung điểm BC, khi đó BC lần lượt vuông góc với các cạnh AM và

DM. Khẳng định đúng là BC vuông góc với mặt phẳng nào dưới đây?

A. (MAD);

B. (ACD);

C. (ABC);

D. (ABD).

Xem đáp án

Đáp án đúng là: A

BC lần lượt vuông góc với các cạnh AM và DM.

Mà AM và DM nằm trong mặt phẳng MAD.

Suy ra BC ^ (MAD).

Câu 6:

Cho hình hộp ABCD.A’B’C’D’. Đẳng thức nào sau đây là sai?

A. $\vec{A B} + \vec{A D} + \vec{A A'} = \vec{A C'};$

B. $\vec{B C} + \vec{C D} + \vec{B B'} = \vec{B D'};$

C. $\vec{C B} + \vec{C D} + \vec{D D'} = \vec{C A'};$

D. $\vec{A D} + \vec{A B} + \vec{A A'} = \vec{A' C} .$

Xem đáp án

Cho hình hộp ABCD.A’B’C’D’. Đẳng thức nào sau đây là sai? (ảnh 1)

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đẳng thức nào đúng?

A. $\vec{S A} + \vec{S D} = \vec{S C} + \vec{S B};$

B. $\vec{S A} + \vec{S C} = \vec{S D} + \vec{S B};$

C. $\vec{S A} + \vec{S C} = \vec{S A} + \vec{S B};$

D. $\vec{S A} + \vec{S B} + \vec{S C} + \vec{S D} = \vec{0} .$

Xem đáp án

Đáp án đúng là: B

O là tâm của hình bình hành ABCD.

M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

$\{\begin{cases} \vec{S A} + \vec{S D} = 2 \vec{S Q} \\ \vec{S C} + \vec{S B} = 2 \vec{S N} \end{cases} \Rightarrow \vec{S A} + \vec{S C} \neq \vec{S D} + \vec{S B}; \vec{S A} + \vec{S C} = \vec{S D} + \vec{S B} = 2 \vec{S O} \vec{S C} \neq \vec{S B} \Rightarrow \vec{S A} + \vec{S C} \neq \vec{S A} + \vec{S B} \vec{S A} + \vec{S B} + \vec{S C} + \vec{S D} = 2 \vec{S M} + 2 \vec{S P} = 4 \vec{S O} .$

Câu 8:

$\lim_{x \to + \infty} x (\sqrt{x^{2} + 2} - x)$ bằng:

A. +¥

B. 0;

C. 2;

D. 1.

Xem đáp án

lim x đến dương vô cùng x( căn x^2+2-x) bằng: (ảnh 1)

Câu 9:

Cho tứ diện ABCD. Gọi P, Q là trung điểm của AB và CD. Chọn khẳng định đúng?

A. $\vec{P Q} = \vec{B C} + \vec{A D};$

B. $\vec{P Q} = \frac{1}{2} (\vec{B C} + \vec{A D});$

C. $\vec{P Q} = \frac{1}{2} (\vec{B C} - \vec{A D});$

D. $\vec{P Q} = \frac{1}{4} (\vec{B C} + \vec{A D}) .$

Xem đáp án

Cho tứ diện ABCD. Gọi P, Q là trung điểm của AB và CD. Chọn khẳng định đúng? (ảnh 1)

Câu 10:

Hàm số

y = \frac{x + 1}{x + 2}

gián đoạn tại điểm nào dưới đây ?

A. x = -1;

B. x = 1;

C. x = -2;

D. x = 2.

Xem đáp án

Đáp án đúng là: C

$y = \frac{x + 1}{x + 2}$ gián đoạn tại x = -2.

Câu 11:

Hàm số $f (x) = \frac{2 x}{x^{2} - 2 x - 3}$ liên tục trên khoảng nào dưới đây ?

A. (-2; 0);

B. (0; 2);

C. (2; 4);

D. (-¥; +¥).

Xem đáp án

Hàm số fx=2x/x^2-2x-3 liên tục trên khoảng nào dưới đây ? (ảnh 1)

Câu 12:

Trong không gian, cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp đường thẳng AB và DD’ ?

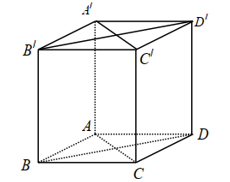
Trong không gian, cho hình lập phương ABCD.A’B’C’D’ (ảnh 1)

A. 120°

B. 60°;

C. 90°;

D. 45°.

Xem đáp án

Đáp án đúng là: C

$(\hat{A B, D D'}) = (\hat{A B, A A'}) = \hat{A' A B} = 90 ° .$

Câu 13:

Phát biểu nào sau đây là sai ?

A. lim qⁿ = 0 ( |q| >1);

B. lim u_n = c (với u_n = c là hằng số );

C. $\lim \frac{1}{n^{k}} = 0 (k > 1);$

D. $\lim \frac{1}{n} = 0.$

Xem đáp án

Đáp án đúng là: A

lim qⁿ = 0 ( |q| >1) (sai vì |q| < 1).

Câu 14:

Cho hai hàm số f (x), g (x) thỏa mãn $\lim_{x \to 1} f (x) = 3$ và $\lim_{x \to 1} [f (x) - 2 g (x)]$ Giá trị của bằng:

A. 1

B. 5

C. -1

D. 6

Xem đáp án

Đáp án đúng là: C

$\lim_{x \to 1} [f (x) - 2 g (x)] = \lim_{x \to 1} f (x) - 2 \lim_{x \to 1} g (x)$

= 3 - 2.2 = -1.

Câu 15:

$\lim_{x \to - \infty} (- x^{4} + 2 x^{2})$ bằng:

A. +¥;

B. -¥;

C. 1;

D. -1.

Xem đáp án

Đáp án đúng là: B

\lim_{x \to - \infty} (- x^{4} + 2 x^{2}) = - \infty .

Câu 16:

Trong bốn giới hạn sau đây, giới hạn nào bằng 0?

A. $\lim \frac{1 - n^{3}}{n^{2} + 2 n};$

B. $\lim \frac{(2 n + 1) {(n - 3)}^{2}}{n - 2 n^{3}};$

C. $\lim \frac{2^{n} + 1}{{3.2}^{n} - 3^{n}};$

D. $\lim \frac{2^{n} + 3}{1 - 2^{n}} .$

Xem đáp án

Đáp án đúng là: C

$\lim \frac{1 - n^{3}}{n^{2} + 2 n} = \lim \frac{\frac{1}{n^{3}} - 1}{\frac{1}{n} + \frac{2}{n^{2}}} = - \infty \lim \frac{(2 n + 1) {(n - 3)}^{2}}{n - 2 n^{3}} = \lim \frac{(2 + \frac{1}{n}) {(1 - \frac{3}{n})}^{2}}{\frac{1}{n^{2}} - 2} = \frac{2.1}{- 2} = - 1 \lim \frac{2^{n} + 1}{{3.2}^{n} - 3^{n}} = \lim \frac{{(\frac{2}{3})}^{n} + {(\frac{1}{3})}^{n}}{3. {(\frac{2}{3})}^{n} - 1} = 0 \lim \frac{2^{n} + 3}{1 - 2^{n}} = \lim \frac{1 + \frac{3}{2^{n}}}{\frac{1}{2^{n}} - 1} = - 1.$ ;

Câu 17:

Giới hạn $\lim_{x \to + \infty} \frac{c x^{2} + a}{x^{2} + b}$ có giá trị bằng:

A. b;

B. c;

C. a;

D. $\frac{a + b}{c} .$

Xem đáp án

Đáp án đúng là: B

$\lim_{x \to + \infty} \frac{c x^{2} + a}{x^{2} + b} = \lim_{x \to + \infty} \frac{c + \frac{a}{x^{2}}}{1 + \frac{b}{x^{2}}} = c .$

Câu 18:

Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?

A. BC ^ AD;

B. AC ^ BC;

C. CD ^ (ABD);

D. AB ^ (ABC).

Xem đáp án

Đáp án đúng là: A

Gọi M là trung điểm của BC.

Tam giác ABC và tam giác DBC là hai tam giác cân lần lượt tại A và D.

Nên AM và DM là đường cao của ABC và DBC.

Suy ra BC ^ (AMD).

Do đó AM ^ AD.

Câu 19:

Cho hình chóp S.ABCD đáy là hình vuông cạnh a, tâm O. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi a là góc tạo bởi đường thẳng SC và mặt phẳng đáy.

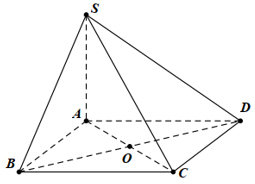
Cho hình chóp S.ABCD đáy là hình vuông cạnh a, tâm O. (ảnh 1)

Mệnh đề nào sau đây đúng?

A. tan a = 1;

B. $\tan α = \sqrt{2};$

C. $\tan α = \sqrt{3};$

D. $\tan α = \frac{\sqrt{2}}{2} .$

Xem đáp án

Đáp án đúng là: B

Ta có (SC, (ABCD)) = (SC, AC) .

Suy ra $\tan α = \tan \hat{S C A} = \frac{S A}{A C} = \frac{2 a}{\sqrt{a^{2} + a^{2}}} = \sqrt{2} .$

Câu 20:

Cho dãy số (u_n) thỏa mãn lim (u_n - 1) = 0. Giá trị của lim u_n bằng:

A. 0;

B. -2;

C. 2;

D. 1.

Xem đáp án

Đáp án đúng là: D

lim (u_n - 1) = 0

Û lim u_n - lim 1 = 0

Û lim u_n = lim 1 = 1.

Câu 21:

$\lim n (\sqrt{n^{2} + 1} - \sqrt{n^{2} - 3})$ bằng bao nhiêu?

A. +¥;

B. 2;

C. -1;

D. 4.

Xem đáp án

Đáp án đúng là: B

\lim n (\sqrt{n^{2} + 1} - \sqrt{n^{2} - 3}) = \lim \frac{n [(n^{2} + 1) - (n^{2} - 3)]}{\sqrt{n^{2} + 1} + \sqrt{n^{2} - 3}} = \lim \frac{4 n}{\sqrt{n^{2} + 1} + \sqrt{n^{2} - 3}} = \lim \frac{4}{\sqrt{1 + \frac{1}{n^{2}}} + \sqrt{1 - \frac{3}{n^{2}}}} = \frac{4}{1 + 1} = 2.

Câu 22:

lim (n + 17) bằng:

A. 1;

B. +¥;

C. 2;

D. -¥.

Xem đáp án

Đáp án đúng là: B

lim (n + 17) = +¥.

Câu 23:

Cho hàm số f (x) thỏa mãn $\lim_{x \to 1^{+}} f (x) = 2$ và . Giá trị của $\lim_{x \to 1} f (x)$ bằng:

A. -1;

B. 2;

C. 1;

D. -2.

Xem đáp án

Đáp án đúng là: B

\lim_{x \to 1} f (x) = \lim_{x \to 1^{+}} f (x) = \lim_{x \to 1^{-}} f (x) = 2.

Câu 24:

$\lim \frac{2 n^{2} - n + 1}{n^{3} + n}$ bằng:

A. 1;

B. +¥;

C. 2;

D. 0.

Xem đáp án

Đáp án đúng là: D

Ta có $\lim \frac{2 n^{2} - n + 1}{n^{3} + n} = \lim \frac{\frac{2}{n} - \frac{1}{n^{2}} + \frac{1}{n^{3}}}{1 + \frac{1}{n^{2}}}$

Do $\lim (\frac{2}{n} - \frac{1}{n^{2}} + \frac{1}{n^{3}}) = 0$

Mà lại có $\lim (1 + \frac{1}{n^{2}}) = 1$

Suy ra $\lim \frac{2 n^{2} - n + 1}{n^{3} + n} = \lim \frac{\frac{2}{n} - \frac{1}{n^{2}} + \frac{1}{n^{3}}}{1 + \frac{1}{n^{2}}} = 0.$

Câu 25:

\lim_{x \to + \infty} (\sqrt{x + 5} - \sqrt{x - 7})

bằng:

A. -¥;

B. +¥;

C. 0;

D. 4.

Xem đáp án

Đáp án đúng là: C

\lim_{x \to + \infty} (\sqrt{x + 5} - \sqrt{x - 7}) = \lim_{x \to + \infty} \frac{(x + 5) - (x - 7)}{\sqrt{x + 5} + \sqrt{x - 7}} = \lim_{x \to + \infty} \frac{12}{\sqrt{x + 5} + \sqrt{x - 7}} = 0.

Câu 26:

Cho hàm số $f (x) = \{\begin{matrix} \frac{3 - x}{\sqrt{x + 1} - 2} k h i x \neq 3 \\ m k h i x = 3 \end{matrix} .$ Hàm số đã cho liên tục tại x = 3 khi m bằng:

A. -4;

B. 4;

C. -1;

D. 1.

Xem đáp án

Cho hàm số fx = 3-x/ căn x+1-2 Hàm số đã cho liên tục tại x  3 khi m bằng: (ảnh 1)

Câu 27:

Mệnh đề nào sau đây sai ?

A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song;

B. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau;

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song;

D. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

Xem đáp án

Đáp án đúng là: A

Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song (sai vì trong không gian chúng còn có thể vuông góc với nhau).

Câu 28:

Cho phương trình -4x³ + 4x - 1 = 0. Tìm khẳng định sai trong các khẳng định sau:

A. Phương trình đã cho có ba nghiệm phân biệt;

B. Phương trình đã cho chỉ có một nghiệm trong khoảng (0; 1);

C. Phương trình đã cho có ít nhất một nghiệm trong (-2; 0);

D. Phương trình đã cho có ít nhất một nghiệm trong

(- \frac{1}{2}; \frac{1}{2}) .

Xem đáp án

Cho phương trình 4x^3 4x + 1 = 0. Tìm khẳng định sai (ảnh 1)

Câu 29:

Biết $\lim_{x \to - 1} f (x) = 4.$ Khi đó $\lim_{x \to - 1} \frac{{(x + 3)}^{4}}{f (x)} = \frac{\lim_{x \to - 1} {(x + 3)}^{4}}{\lim_{x \to - 1} f (x)}$ có giá trị bằng:

A. 4;

B. 0;

C. +¥;

D. $\frac{1}{4} .$

Xem đáp án

Biết lĩm đến -1 f(x)=4 Khi đó lim x đến -1 x+3^/f(x) (ảnh 1)

Câu 30:

Kết quả đúng của $\lim_{x \to + \infty} \frac{x - 1}{\sqrt{x^{2} - 1}}$ là:

A. -1;

B. 0;

C. +¥;

D. 1.

Xem đáp án

Đáp án đúng là: D

Ta có

$\lim_{x \to + \infty} \frac{x - 1}{\sqrt{x^{2} - 1}} = \lim_{x \to + \infty} \frac{1 - \frac{1}{x}}{\sqrt{1 - \frac{1}{x^{2}}}} = 1.$

Câu 31:

Cho hình chóp S.ABCD đáy là hình vuông, tâm O, cạnh bên SA vuông góc với đáy. Khi đó, cạnh BD không vuông góc với cạnh nào sau đây?

A. SA;

B. SO;

C. SB;

D. AC.

Xem đáp án

Cho hình chóp S.ABCD đáy là hình vuông, tâm O, cạnh (ảnh 1)

Câu 32:

Cho hình lập phương ABCD.A’B’C’D’. Tìm góc giữa hai vectơ $\vec{A D'}$ và $\vec{B D} .$

A. 45°;

B. 30°

C. 60°;

D. 120

Xem đáp án

Đáp án đúng là: C

Ta có $(\hat{\vec{A D'}, \vec{B D}}) = (\hat{\vec{A D'}, \vec{B' D'}}) = (\hat{\vec{A D'}, \vec{D' B'}})$

Suy ra $\hat{A D' B'} = 60 °$

(do tam giác AB’D’ đều có AB’ = B’D’ = AD’).

Câu 33:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai?

A. BC ^ (SAB);

B. AC ^ (SBD);

C. BD ^ (SAC);

D. CD ^ (SAD).

Xem đáp án

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai? (ảnh 1)

Câu 34:

Cho hàm số: Khi đó

f (x) = \{\begin{matrix} x^{2} - 3 x + 1 k h i x < 2 \\ 5 x - 3 k h i x \geq 2 \end{matrix} .

bằng

A. -13;

B. 7;

C. -1;

D. 11.

Xem đáp án

Đáp án đúng là: C

$\lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{-}} (x^{2} - 3 x + 1) = 2^{2} - 3.2 + 1 = - 1.$

Câu 35:

Khẳng định nào sau đây là khẳng định sai?

A. Nếu d ^ (a) và a // (a) thì a ^ d;

B. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (a) thì d vuông góc với bất kỳ đường thẳng nào nằm trong mặt phẳng (a).

C. Nếu d ^ (a) thì d vuông góc với hai đường thẳng nằm trong (a);

D. Nếu đường thẳng d vuông góc với hai đường thẳng trong mặt phẳng (α) thì d ^ (a)

Xem đáp án

Đáp án đúng là: D

+ Nếu d ^ (a) và a // (a) thì a ^ d (Đúng)

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (a) thì d vuông góc với bất kỳ đường thẳng nào nằm trong mặt phẳng (a) (Đúng)

+ Nếu d ^ (a) thì d vuông góc với hai đường thẳng nằm trong (a) (Đúng)

+ Nếu đường thẳng d vuông góc với hai đường thẳng trong mặt phẳng (α) thì d ^ (a) (Sai vì hai đường thẳng đấy phải cắt nhau).

Câu 36:

a) Tính: $\lim (n - \sqrt{n^{2} + 2 n + 3}) .$

b) Tính giới hạn: $\lim_{x \to 0} (\frac{\sqrt{1 + 2 x} - \sqrt[3]{1 + 3 x}}{x^{2}}) .$

Xem đáp án

a)

$\lim (n - \sqrt{n^{2} + 2 n + 3}) = \lim (\frac{n^{2} - (n^{2} + 2 n + 3)}{n + \sqrt{n^{2} + 2 n + 3}}) = \lim (\frac{- 2 n - 3}{n + \sqrt{n^{2} + 2 n + 3}}) = \lim (\frac{- 2 - \frac{3}{n}}{1 + \sqrt{1 + \frac{2}{n} + \frac{3}{n^{2}}}}) = \frac{- 2}{1 + 1} = - 1$

Câu 37:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tâm O, cạnh BC = a, SA = SB = SC = SD = 2a . Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA.

a) Chứng minh: SO ^ (ABCD).

b) Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).

Xem đáp án

a)

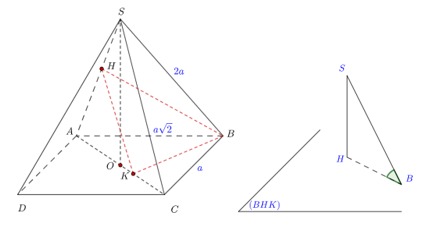
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tâm (ảnh 1)

+ Xét tam giác SAC có SA = SC = 2a nên tam giác SAC cân tại S, có O là trung điểm của AC nên SO là đường trung tuyến và cũng là đường cao của tam giác SAC

Suy ra SO ^ AC (1)

+ Xét tam giác SAC có SB = SD = 2a nên tam giác SBD cân tại S, có O là trung điểm của BD nên SO là đường trung tuyến và cũng là đường cao của tam giác SBD

Suy ra SO ^ BD (2)

Từ (1) và (2) nên ta có SO ^ (ABCD)

b) Ta có:

Từ đó suy ra BK ^ SH

Mà KH ^ SH

Nên ta có SH ^ (BKH) Þ (SB, (BKH)) = (SB, HB) = a

Ta cũng suy ra được SH ^ BH

$\cos \hat{S B A} = \frac{S B^{2} + B A^{2} - S A^{2}}{2. S B . B A} = \frac{{(2 a)}^{2} + {(a \sqrt{2})}^{2} - {(2 a)}^{2}}{2.2 a . a \sqrt{2}} = \frac{\sqrt{2}}{4} \Rightarrow \sin \hat{S B A} = \sqrt{1 - {(\cos \hat{S B A})}^{2}} = \frac{\sqrt{14}}{4}$

Ta có:

$S_{S A B} = \frac{1}{2} S B . A B . \sin \hat{S B A} = \frac{1}{2} H B . A S \Rightarrow H B = \frac{S B . A B . \sin \hat{S B A}}{S A} = \frac{2 a . a \sqrt{2} . \frac{\sqrt{14}}{4}}{2 a} = \frac{a \sqrt{7}}{2} \cos α = \frac{H B}{S B} = \frac{\frac{a \sqrt{7}}{2}}{2 a} = \frac{\sqrt{7}}{4} .$

Câu 38:

Chứng minh phương trình: (1 - m²)(x + 1)³ + x² - x - 3 = 0 có nghiệm với mọi m.

Xem đáp án

Đặt f (x) = (1 - m²)(x + 1)³ + x² - x - 3 = 0 liên tục trên ℝ

Ta có:

+ f (0) = (1 - m²) - 3 = -2 - m²< 0 ("m Î ℝ)

+ f (-2) = - (1 - m²) + (-2)² - (-2) - 3

= m² - 1 + 4 + 2 - 3 = m² + 2 > 0 ("m Î ℝ)

Xét f (-2). f (0) = (m² + 2).(-2 - m²) = - (m² + 2)² < 0 ("m Î ℝ)

Nên suy ra phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0)

Từ đây có thể kết luận được phương trình: (1 - m²)(x + 1)³ + x² - x - 3 = 0 có nghiệm với mọi m.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 7)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương