Cho tứ diện ABCD với đáy BCD là tam giác vuông cân tại C. Các điểm M, N, P, Q lần lượt là trung điểm của AB, AC, BC, CD. Góc giữa MN và PQ bằng
A. 45°;
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
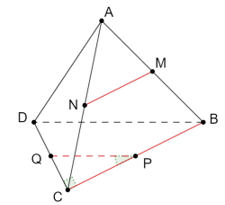
Vì M, N lần lượt là trung điểm của các cạnh AB, AC.
Nên MN là đường trung bình của tam giác ABC. Suy ra MN // BC.
Ta có MN // BC nên góc giữa MN và PQ là góc giữa BC và PQ.
Do đó góc giữa MN và PQ là .
Mà Q, P lần lượt là trung điểm của các cạnh CD, BC nên QP là đường trung bình của tam giác BCD.
Từ đó suy ra QP // BD nên góc (hai góc đồng vị và với tam giác
BCD vuông cân tại C).
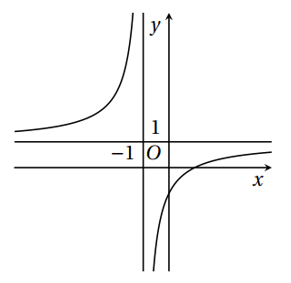
Hình vẽ sau là đồ thị của một hàm số y = f (x). Hãy quan sát đồ thị và cho biết lần lượt có giá trị bằng
Cho hình lập phương ABCD.A1B1C1D1. Góc giữa hai đường thẳng AC và DA1 bằng
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng
Cho hình chóp S.ABCD có SA vuông góc với đáy và SA = 1, đáy là hình vuông cạnh x (0 < x £ 1). Tính giá trị lớn nhất của diện tích thiết diện của hình chóp đã cho khi cắt bởi mặt phẳng đi qua A và vuông góc với SC.
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng?
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Tính số đo góc giữa hai đường thẳng MN và CD.
Cho hình chóp S.ABC có đáy là tam giác vuông tại B và SA ^ (ABC). Mệnh đề nào sau đây đúng?