Câu hỏi:

20/07/2024 190

Cho tứ diện ABCD có trọng tâm G. Chọn khẳng định đúng?

A. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 3 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

B. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 4 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

Đáp án chính xác

C. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 6 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

D. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 2 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

Chọn đáp án B

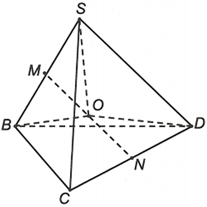
Ta có $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2}$

$= {(\vec{A G} + \vec{G B})}^{2} + {(\vec{A G} + \vec{G C})}^{2} + {(\vec{A G} + \vec{G D})}^{2} + {(\vec{B G} + \vec{G C})}^{2} + {(\vec{B G} + \vec{G D})}^{2} + {(\vec{C G} + \vec{G D})}^{2}$

$= 3 A G^{2} + 3 B G^{2} + 3 C G^{2} + 3 D G^{2} + 2 (\vec{A G} . \vec{G B} + \vec{A G} . \vec{G C} + \vec{A G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{C G} . \vec{G D}) (1)$

Mà $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0} \Leftrightarrow {(\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D})}^{2} = 0$

$\Leftrightarrow G A^{2} + G B^{2} + G C^{2} + G D^{2}$

$= 2 (\vec{A G} . \vec{G B} + \vec{A G} . \vec{G C} + \vec{A G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{C G} . \vec{G D}) (2)$

Từ (1) và (2) ta có $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 4 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số $\frac{S M}{S O}$ sao cho biểu thức $P = M S^{2} + M A^{2} + M B^{2} + M C^{2} + M D^{2}$ nhỏ nhất bằng

Xem đáp án » 21/10/2022 589

Câu 2:

b) Nếu ABCD là hình chữ nhật thì ${\vec{S A}}^{2} + {\vec{S C}}^{2} = {\vec{S B}}^{2} + {\vec{S D}}^{2}$

Xem đáp án » 21/10/2022 285

Câu 3:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C} = 2 \vec{M N}$

Xem đáp án » 21/10/2022 241

Câu 4:

Cho hình lăng trụ tam giác ABC.A'B'C' có $\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}, \vec{A C} = \vec{c}$ . Hãy phân tích các vectơ $\vec{B^{'} C}, \vec{B C^{'}}$ qua các vectơ $\vec{a}, \vec{b}, \vec{c}$ .

Xem đáp án » 21/10/2022 239

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

a) Chứng minh $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Xem đáp án » 21/10/2022 237

Câu 6:

Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ không đồng phẳng. xét các vectơ $\vec{x} = 2 \vec{a} + \vec{b}, \vec{y} = \vec{a} - \vec{b} - \vec{c}, \vec{z} = - 3 \vec{b} - 2 \vec{c}$ . Chọn khẳng định đúng?

Xem đáp án » 21/10/2022 220

Câu 7:

Cho tứ diện ABCD, O là trọng tâm tam giác BCD, M là trung điểm của AD. Khẳng định nào dưới đây đúng?

Xem đáp án » 21/10/2022 214

Câu 8:

Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho $A M = 2 M D, B C = 3 N C$ . Chứng minh ba vectơ $\vec{A B}, \vec{C D}, \vec{M N}$ đồng phẳng.

Xem đáp án » 21/10/2022 212

Câu 9:

Cho tứ diện SABC. Đặt $\vec{S A} = \vec{a}, \vec{S B} = \vec{b}, \vec{S C} = \vec{c}$ . Gọi M là trung điểm của SA, N là điểm trên cạnh BC sao cho $N C = 3 N B$ . Phân tích vectơ $\vec{M N}$ theo ba vectơ $\vec{a}, \vec{b}$ và $\vec{c}$ ta được

Xem đáp án » 21/10/2022 207

Câu 10:

Cho lăng trụ tam giác ABC.A'B'C'. Gọi I, K lần lượt là trung điểm của BB', A'C'. Điểm M thuộc cạnh B'C' sao cho $\vec{M B^{'}} = k \vec{M C^{'}}$ . Tìm k để bốn điểm $A, I, M, K$ đồng phẳng.

Xem đáp án » 21/10/2022 207

Câu 11:

Trong các mệnh đề sau đây, mệnh đề nào là đúng?

Xem đáp án » 21/10/2022 203

Câu 12:

Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Cho $A B = 2 a, C D = 2 b, E F = 2 c$ . Với M là một điểm tùy ý, tổng $M A^{2} + M B^{2}$ bằng

Xem đáp án » 21/10/2022 202

Câu 13:

Cho hình chóp S.ABC. Lấy điểm M và N sao cho $\vec{M S} = - 2 \vec{M A}$ và $\vec{N C} = - 2 \vec{N B}$ . Chứng minh rằng ba vectơ $\vec{A B}, \vec{M N}, \vec{S C}$ đồng phẳng.

Xem đáp án » 21/10/2022 200

Câu 14:

Cho tứ diện ABCD, M và N là các điểm lần lượt thuộc AB và CD sao cho $\vec{M A} = - 2 \vec{M B}, \vec{N D} = - 2 \vec{N C}$ ; các điểm I, J, K lần lượt thuộc $A D, M N, B C$ sao cho $\vec{I A} = k . \vec{I D}, \vec{J M} = k . \vec{J N}, \vec{K B} = k . \vec{K C}$ . Chứng minh rằng các điểm I, J, K thẳng hàng.

Xem đáp án » 21/10/2022 198

Câu 15:

Cho tứ diện S.ABC có $S A = S B = S C = A B = A C = a, B C = a \sqrt{2}$ . Tích vô hướng giữa $\vec{S C} . \vec{A B}$ bằng

Xem đáp án » 21/10/2022 197

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản

7 đề 40133 lượt thi Thi thử
93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải

5 đề 29987 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn nâng cao

4 đề 24838 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn cơ bản

4 đề 24168 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao

6 đề 19772 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác cơ bản

5 đề 18701 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác nâng cao

6 đề 18500 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm cơ bản

6 đề 17739 lượt thi Thi thử
Trắc nghiệm Hàm số lượng giác có đáp án

2 đề 15912 lượt thi Thi thử
Bài tập Lượng Giác cơ bản , nâng cao có lời giải

13 đề 12475 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Cho hàm số $f (x) = {(3 x^{2} - 2 x - 1)}^{9}$ . Tính đạo hàm cấp 6 của hàm số tại điểm x=0.

327 21/10/2022 Xem đáp án
Cho hàm số $y = \sin \frac{x}{2}$ . Đạo hàm $y^{(n)}$ là

236 21/10/2022 Xem đáp án
Cho hàm số y=sin3x.cosx-sin2x . Giá trị của $y^{(10)} (\frac{π}{3})$ gần nhất với số nào dưới đây?

331 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=sin2x là

234 21/10/2022 Xem đáp án
Đạo hàm cấp 2021 của hàm số f(x)=cos(x+a) là

236 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{x}{x^{2} + 5 x + 6}$ là

243 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{2 x + 1}{x^{2} - 3 x + 2}$ là

289 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \sqrt{2 x + 1}$ là

297 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=cos2x là

368 21/10/2022 Xem đáp án
Cho hàm số $y = \sin^{2} 2 x$ . Giá trị của biểu thức $y^{(3)} + {y^{'}}^{'} + 16 y^{'} + 16 y - 8$ là

222 21/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Cho tứ diện ABCD có trọng tâm G. Chọn khẳng định đúng?

A. AB2+AC2+AD2+BC2+BD2+CD2=3GA2+GB2+GC2+GD2

B. AB2+AC2+AD2+BC2+BD2+CD2=4GA2+GB2+GC2+GD2

C. AB2+AC2+AD2+BC2+BD2+CD2=6GA2+GB2+GC2+GD2

D. AB2+AC2+AD2+BC2+BD2+CD2=2GA2+GB2+GC2+GD2

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số SMSO sao cho biểu thức P=MS2+MA2+MB2+MC2+MD2 nhỏ nhất bằng

Câu 2:

b) Nếu ABCD là hình chữ nhật thì SA→2+SC→2=SB→2+SD→2

Câu 3:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng AC→+BD→=AD→+BC→=2MN→

Câu 4:

Cho hình lăng trụ tam giác ABC.A'B'C' có AA'→=a→,AB→=b→,AC→=c→ . Hãy phân tích các vectơ B'C→,BC'→ qua các vectơ a→,b→,c→.

Câu 5:

A. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 3 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

B. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 4 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

C. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 6 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

D. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 2 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số $\frac{S M}{S O}$ sao cho biểu thức $P = M S^{2} + M A^{2} + M B^{2} + M C^{2} + M D^{2}$ nhỏ nhất bằng

b) Nếu ABCD là hình chữ nhật thì ${\vec{S A}}^{2} + {\vec{S C}}^{2} = {\vec{S B}}^{2} + {\vec{S D}}^{2}$

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C} = 2 \vec{M N}$

Cho hình lăng trụ tam giác ABC.A'B'C' có $\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}, \vec{A C} = \vec{c}$ . Hãy phân tích các vectơ $\vec{B^{'} C}, \vec{B C^{'}}$ qua các vectơ $\vec{a}, \vec{b}, \vec{c}$ .