Câu hỏi:

12/07/2024 108

Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề

(I). Nếu ABCD là hình bình hành thì $\vec{S A} + \vec{S B} + \vec{S C} + \vec{S D} = 4 \vec{S O}$ .

(II). Nếu $\vec{S A} + \vec{S B} + \vec{S C} + \vec{S D} = 4 \vec{S O}$ thì ABCD là hình bình hành.

Mệnh đề nào đúng?

A. Chỉ (I).

B. Chỉ (II).

C. Không có.

D. Cả (I) và (II).

Đáp án chính xác

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

Chọn đáp án D

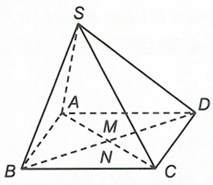
$Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề (I). Nếu ABCD là hình\ (ảnh 1)$

Gọi M, N lần lượt là trung điểm của AC và BD. Do O là giao điểm của AC và BD nên

$\vec{S A} + \vec{S B} + \vec{S C} + \vec{S D} = 4 \vec{S O}$

$\Leftrightarrow (\vec{O S} + \vec{S A}) + (\vec{O S} + \vec{S C}) + (\vec{O S} + \vec{S B}) + (\vec{O S} + \vec{S D}) = \vec{0}$

$\Leftrightarrow (\vec{O A} + \vec{O C}) + (\vec{O B} + \vec{O D}) = \vec{0}$

$\Leftrightarrow 2 \vec{O M} + 2 \vec{O N} = \vec{0} \Leftrightarrow \vec{O M} = \vec{O N} \Leftrightarrow O \equiv M \equiv N$

$\Leftrightarrow A B C D$ là hình bình hành.

Vậy mệnh đề (I) và (II) đều đúng.

Bình luận: Để chứng minh mệnh đề (I) và (II) đúng, ta áp dụng: Cho $A \in a, B \in b$ và $\{O\} = a \cap b$ .

Khi đó $\vec{O A} = \vec{O B} \Leftrightarrow O \equiv A \equiv B$ .

Chứng minh: Nếu A không trùng O thì B không trùng O (do $\vec{O A} = \vec{O B}$ ) $\Rightarrow O A \equiv a$ và $O B \equiv b$

Nhưng $\vec{O A} = \vec{O B} \Rightarrow O, A, B$ thẳng hàng $\Rightarrow a \equiv b \Rightarrow a \cap b = a$ (trái với giả thiết $O = a \cap b$ )

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số $\frac{S M}{S O}$ sao cho biểu thức $P = M S^{2} + M A^{2} + M B^{2} + M C^{2} + M D^{2}$ nhỏ nhất bằng

Xem đáp án » 21/10/2022 575

Câu 2:

b) Nếu ABCD là hình chữ nhật thì ${\vec{S A}}^{2} + {\vec{S C}}^{2} = {\vec{S B}}^{2} + {\vec{S D}}^{2}$

Xem đáp án » 21/10/2022 268

Câu 3:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C} = 2 \vec{M N}$

Xem đáp án » 21/10/2022 237

Câu 4:

Cho hình lăng trụ tam giác ABC.A'B'C' có $\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}, \vec{A C} = \vec{c}$ . Hãy phân tích các vectơ $\vec{B^{'} C}, \vec{B C^{'}}$ qua các vectơ $\vec{a}, \vec{b}, \vec{c}$ .

Xem đáp án » 21/10/2022 228

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

a) Chứng minh $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Xem đáp án » 21/10/2022 227

Câu 6:

Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ không đồng phẳng. xét các vectơ $\vec{x} = 2 \vec{a} + \vec{b}, \vec{y} = \vec{a} - \vec{b} - \vec{c}, \vec{z} = - 3 \vec{b} - 2 \vec{c}$ . Chọn khẳng định đúng?

Xem đáp án » 21/10/2022 216

Câu 7:

Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho $A M = 2 M D, B C = 3 N C$ . Chứng minh ba vectơ $\vec{A B}, \vec{C D}, \vec{M N}$ đồng phẳng.

Xem đáp án » 21/10/2022 208

Câu 8:

Cho tứ diện ABCD, O là trọng tâm tam giác BCD, M là trung điểm của AD. Khẳng định nào dưới đây đúng?

Xem đáp án » 21/10/2022 207

Câu 9:

Cho tứ diện SABC. Đặt $\vec{S A} = \vec{a}, \vec{S B} = \vec{b}, \vec{S C} = \vec{c}$ . Gọi M là trung điểm của SA, N là điểm trên cạnh BC sao cho $N C = 3 N B$ . Phân tích vectơ $\vec{M N}$ theo ba vectơ $\vec{a}, \vec{b}$ và $\vec{c}$ ta được

Xem đáp án » 21/10/2022 203

Câu 10:

Trong các mệnh đề sau đây, mệnh đề nào là đúng?

Xem đáp án » 21/10/2022 200

Câu 11:

Cho lăng trụ tam giác ABC.A'B'C'. Gọi I, K lần lượt là trung điểm của BB', A'C'. Điểm M thuộc cạnh B'C' sao cho $\vec{M B^{'}} = k \vec{M C^{'}}$ . Tìm k để bốn điểm $A, I, M, K$ đồng phẳng.

Xem đáp án » 21/10/2022 200

Câu 12:

Cho hình chóp S.ABC. Lấy điểm M và N sao cho $\vec{M S} = - 2 \vec{M A}$ và $\vec{N C} = - 2 \vec{N B}$ . Chứng minh rằng ba vectơ $\vec{A B}, \vec{M N}, \vec{S C}$ đồng phẳng.

Xem đáp án » 21/10/2022 195

Câu 13:

Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Cho $A B = 2 a, C D = 2 b, E F = 2 c$ . Với M là một điểm tùy ý, tổng $M A^{2} + M B^{2}$ bằng

Xem đáp án » 21/10/2022 195

Câu 14:

Cho tứ diện ABCD, M và N là các điểm lần lượt thuộc AB và CD sao cho $\vec{M A} = - 2 \vec{M B}, \vec{N D} = - 2 \vec{N C}$ ; các điểm I, J, K lần lượt thuộc $A D, M N, B C$ sao cho $\vec{I A} = k . \vec{I D}, \vec{J M} = k . \vec{J N}, \vec{K B} = k . \vec{K C}$ . Chứng minh rằng các điểm I, J, K thẳng hàng.

Xem đáp án » 21/10/2022 194

Câu 15:

Cho hình chóp S.ABC có $\vec{S A} = \vec{a}, \vec{S B} = \vec{b}, \vec{S C} = \vec{c}$ và các điểm M, N lần lượt là trung điểm của các cạnh AB, SC. Các điểm P, Q trên các đường thẳng SA, BN sao cho $P Q / / C M$ . Biểu diễn vectơ $\vec{P Q}$ theo ba vectơ $\vec{a}, \vec{b}, \vec{c}$ được kết quả

Xem đáp án » 21/10/2022 192

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản

7 đề 40133 lượt thi Thi thử
93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải

5 đề 29987 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn nâng cao

4 đề 24838 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn cơ bản

4 đề 24168 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao

6 đề 19772 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác cơ bản

5 đề 18701 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác nâng cao

6 đề 18500 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm cơ bản

6 đề 17739 lượt thi Thi thử
Trắc nghiệm Hàm số lượng giác có đáp án

2 đề 15912 lượt thi Thi thử
Bài tập Lượng Giác cơ bản , nâng cao có lời giải

13 đề 12475 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Cho hàm số $f (x) = {(3 x^{2} - 2 x - 1)}^{9}$ . Tính đạo hàm cấp 6 của hàm số tại điểm x=0.

320 21/10/2022 Xem đáp án
Cho hàm số $y = \sin \frac{x}{2}$ . Đạo hàm $y^{(n)}$ là

226 21/10/2022 Xem đáp án
Cho hàm số y=sin3x.cosx-sin2x . Giá trị của $y^{(10)} (\frac{π}{3})$ gần nhất với số nào dưới đây?

323 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=sin2x là

225 21/10/2022 Xem đáp án
Đạo hàm cấp 2021 của hàm số f(x)=cos(x+a) là

227 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{x}{x^{2} + 5 x + 6}$ là

234 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{2 x + 1}{x^{2} - 3 x + 2}$ là

281 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \sqrt{2 x + 1}$ là

288 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=cos2x là

354 21/10/2022 Xem đáp án
Cho hàm số $y = \sin^{2} 2 x$ . Giá trị của biểu thức $y^{(3)} + {y^{'}}^{'} + 16 y^{'} + 16 y - 8$ là

214 21/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề (I). Nếu ABCD là hình bình hành thì SA→+SB→+SC→+SD→=4SO→ . (II). Nếu SA→+SB→+SC→+SD→=4SO→ thì ABCD là hình bình hành. Mệnh đề nào đúng?

A. Chỉ (I).

B. Chỉ (II).

C. Không có.

D. Cả (I) và (II).

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số SMSO sao cho biểu thức P=MS2+MA2+MB2+MC2+MD2 nhỏ nhất bằng

Câu 2:

b) Nếu ABCD là hình chữ nhật thì SA→2+SC→2=SB→2+SD→2

Câu 3:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng AC→+BD→=AD→+BC→=2MN→

Câu 4:

Cho hình lăng trụ tam giác ABC.A'B'C' có AA'→=a→,AB→=b→,AC→=c→ . Hãy phân tích các vectơ B'C→,BC'→ qua các vectơ a→,b→,c→.

Câu 5:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số $\frac{S M}{S O}$ sao cho biểu thức $P = M S^{2} + M A^{2} + M B^{2} + M C^{2} + M D^{2}$ nhỏ nhất bằng

b) Nếu ABCD là hình chữ nhật thì ${\vec{S A}}^{2} + {\vec{S C}}^{2} = {\vec{S B}}^{2} + {\vec{S D}}^{2}$

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C} = 2 \vec{M N}$

Cho hình lăng trụ tam giác ABC.A'B'C' có $\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}, \vec{A C} = \vec{c}$ . Hãy phân tích các vectơ $\vec{B^{'} C}, \vec{B C^{'}}$ qua các vectơ $\vec{a}, \vec{b}, \vec{c}$ .