Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Tìm giao tuyến của hai mặt phẳng (ABD) và (MNP)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
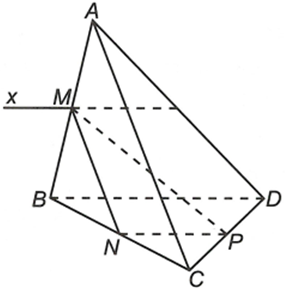
Ta có nên
Xét ∆BCD, có NP là đường trung bình => NP // BD
Từ đó suy ra , trong đó Mx // NP // BD
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Gọi I, J lần lượt là trung điểm của AD và BC, G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (IJG) là
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng:
a)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)
b) Gọi M là trung điểm BC, đường thẳng d qua M và song song SD.
Tìm giao điểm của d và mặt phẳng (SAB)
Cho tứ diện ABCD, gọi M và N lần lượt là trung điểm của AB và AC. E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là