Giải bởi qa.haylamdo.com
Đáp án D
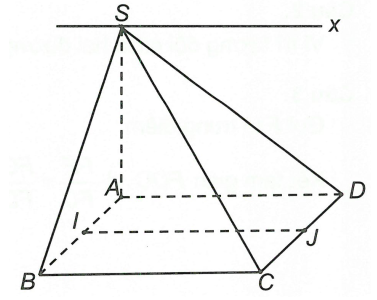
Ta có: giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng đi qua S và song song với AB. Mà I, J lần lượt là trung điểm của AB và CD nên IJ // AB.
Vậy giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với IJCho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Gọi I, J lần lượt là trung điểm của AD và BC, G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (IJG) là
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng:
a)
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Tìm giao tuyến của hai mặt phẳng (ABD) và (MNP)
b) Gọi M là trung điểm BC, đường thẳng d qua M và song song SD.
Tìm giao điểm của d và mặt phẳng (SAB)
Cho tứ diện ABCD, gọi M và N lần lượt là trung điểm của AB và AC. E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là
