A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: C
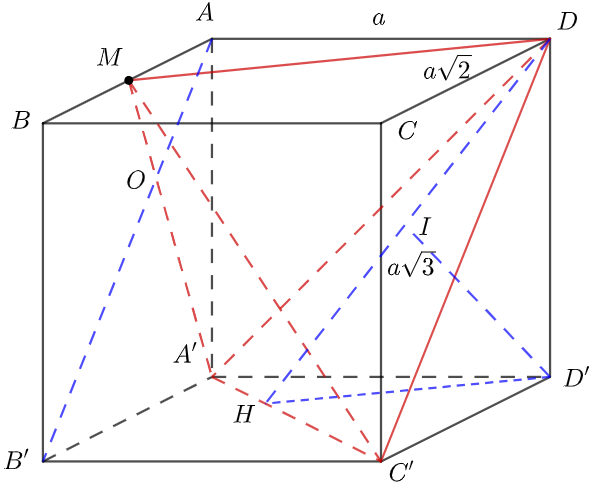
Áp dụng định lý Pytago ta có
Sử dụng công thức Hê-rông tính diện tích tam giác A’DC’
Ta có p là nửa chu vi tam giác A’DC’ với
Suy ra (*)
Thay các giá trị vào (*) ta được
Kẻ D’H A’C’ (H A’C’)
D’I DH (I DH)
Vậy khoảng cách từ D’ đến A’DC’ chính bằng ID’
Áp dụng hệ thức lượng trong tam giác vuông ta có
Lại có, MA // A’B’ nên theo Ta-lét ta có
Kết hợp điều kiện AB’ // DC’
2dM/(A’DC’) = 3dO/(A’DC’)
= 3dA/(A’DC’) = 3dD’/(A’DC’) = 3ID’
Suy ra
Trong mặt phẳng tọa độ Oxy, gọi (C) là đồ thị của hàm số . Phương trình tiếp tuyến của (C) tại giao điểm của đồ thị (C) với trục hoành là
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
Tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (-; -2) là
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD và điểm O tùy ý trên mặt phẳng (BCD). Thể tích tứ diện OMNP bằng
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin3 x + 9cos2 x + 6sin x -10. Giá trị của tích M.m bằng
Trong không gian tọa độ Oxyz, gọi (P) là mặt phẳng đi qua 2 điểm A(0; 1; -2), B(2; 1; 0) sao cho khoảng cách từ gốc tọa độ O đến (P) lớn nhất. Phương trình của mặt phẳng (P) là
Cho hàm số f (x) liên tục và có đạo hàm trên [0; 1]. Biết và f (0) = f (1) = 7. Giá trị của tích phân bằng
Gọi F (x) là một nguyên hàm của hàm số f (x) = ex thỏa mãn F (0) = 2. Giá trị của F (1) bằng