A.
B. 10
C. 5
D.
Giải bởi qa.haylamdo.com
Đáp án đúng là: D
Giả sử: z = a + bi (a, b ∈ ℝ)
Þ = a – bi
Þ . z = (a + bi)(a – bi) = a2 + b2
Ta có: (
+ 2i). (z − 4)
= . z – 4 + 2iz – 8i
= a2 + b2 – 4. (a – bi) + 2i. (a + bi) – 8i
= a2 + b2 – 4a + 4bi + 2ai + 2bi2 – 8i
= a2 + b2 – 4a – 2b + (4b + 2a – 8). i
Vì ( + 2i). (z − 4) là số thuần ảo nên a2 + b2 – 4a – 2b = 0
Û (a – 2)2 + (b – 1)2 = 5
Û |a – 2 + (b – 1).i| =
Û |a + bi – 2 – i| =
Û |z – 2 – i| =
Ta có: w = (1 + i). z + 1 − 2i
Þ w = (1 + i). z – (1 + i).(2 + i) + 1 − 2i + (1 + i).(2 + i)
Þ w = (1 + i). (z – 2 – i) + 1 − 2i + 2 + i + 2i + i2
Þ w = (1 + i). (z – 2 – i) + 1 − 2i + 2 + 3i – 1
Þ w = (1 + i). (z – 2 – i) + 2 + i
Þ w – 2 – i = (1 + i). (z – 2 – i)
Þ |w – 2 – i| = |(1 + i). (z – 2 – i)|
Þ |w – 2 – i| = |(1 + i)|. |(z – 2 – i)|
Þ |w – 2 – i| =
Gọi w = x + yi
Þ |x + yi − 2 – i| =
Þ |x – 2 + (y – 1)i| =
Þ (x − 2)2 + (y – 1)2 = 10
Vậy nên tập hợp điểm biểu diễn số phức w = (1 + i). z + 1 − 2i là đường tròn có bán kính bằng
Trong không gian Oxyz, đường thẳng đi qua hai điểm A (1; 0; 2) và B (4; 1; 0) có phương trình tham số là
Trong không gian Oxyz, cho đường thẳng d: = = . Mặt phẳng (P) vuông góc với đường thẳng d, có vectơ pháp tuyến là
Khi tìm nguyên hàm , bằng cách đặt t = ta được nguyên hàm nào sau đây?
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = , trục hoành và các đường thẳng x = 0, x = . Khối tròn xoay tạo thành khi quay (H) quanh trục hoành có thể tích bằng
Trên tập số phức, cho số phức z có biểu diễn hình học là điểm M ở hình vẽ sau.
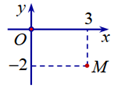
Khẳng định nào sau đây đúng?
Trong hệ trục tọa độ Oxyz cho điểm hai điểm A(1; 2; 3), B(0; 1; −6) và mp (P): 4x − y + 2z + 13 = 0. Gọi (d) là một đường thẳng thuộc (P), (d) đi qua B. Khi khoảng cách từ A đến (d) đạt giá trị nhỏ nhất. Tìm vectơ chỉ phương của đường thẳng (d)
