Trong không gian Oxyz , cho ba điểm A(2; -2; 4), B(-3; 3; -1), C(−1; −1; −1) và mặt phẳng (P): 2x - y + 2z + 8 = 0. Xét điểm M thay đổi thuộc (P), tìm giá trị nhỏ nhất của biểu thức T = 2MA2 + MB2 - MC2.
A. 102;
B. 35;
C. 105;
Giải bởi qa.haylamdo.com
Đáp án đúng là: A
Gọi I là điểm thỏa mãn:
Suy ra I(1; 0; 4)
Khi đó, với mọi điểm M(x; y; z) Î (P), ta luôn có
= 2MI2 + (2IA2 + IB2 - IC2) = 2MI2 + 30
Do đó, T đạt GTNN ⇔ MI đạt GTNN ⇔ MI ^ (P)
Ta có:
Vậy Tmin = 2.62 + 30 = 102.
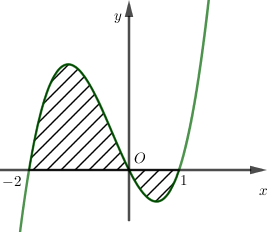
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = - 2, x = 1 như hình vẽ dưới. Khẳng định nào sau đây đúng
Gọi z1, z2 là hai nghiệm phức của phương trình z2 - 2z +7 = 0. Tính P = |z1|2 + |z2|2.
Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số ; y = x - 2 và trục hoành.
Cho số phức z có phần thực bằng -3 và phần ảo bằng 5. Modul của số phức 2 - iz là
Trong không gian Oxyz, cho đường thẳng và điểm
A(1; -2; 0). Tìm bán kính của mặt cầu có tâm I nằm trên d, đi qua A và tiếp xúc với mặt phẳng (P): 2x - 2y + z - 5 = 0.
Cho hai số phức z1 = 3 - 7i và z2 = 2 - 3i. Tìm số phức z = z1 – z2.
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = 2x, y = 0, x = -1, x = 3. Mệnh đề nào dưới đây đúng?
Biết 1 - 2i là một nghiệm của phương trình z2 + az + b = 0, a, b Î ℝ. Tính a - b.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số y = 2x - x2 và y = 2 - x.
Cho số phức z thỏa mãn |z - 2 + i| = |z + 2i|. Trong mặt phẳng phức, tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình nào sau đây?
Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x - 4y + 2z - 3 = 0. Viết phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.
