Cho hình bình hành ABCD, biết A( -2; 1) và phương trình đường thẳng CD là 3x-4y -5= 0. Phương trình tham số của đường thẳng AB là:
A. 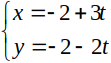
B. 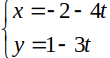
C. 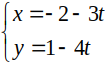
D. 
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn B
Vì ABCD là hình bình hành nên AB//CD
do đó AB đi qua A và nhận vtpt của CD là (3; -4) làm vtpt.
Suy ra đường thẳng AB có vtcp (-4; -3) nên phương trình tham số của đường thẳng AB là

Tìm tọa độ giao điểm của hai đường thẳng sau và d2 : x- y + 1= 0.
Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a) : 4x-3y +5= 0 Và (b) : 3x + 4y -5= 0. Biết hình chữ nhật có đỉnh A( 2 ;1). Diện tích của hình chữ nhật là:
Với giá trị nào của m hai đường thẳng sau đây vuông góc nhau ?
∆1 : mx+ y-19 = 0 và ∆2 : (m-1) x+ (m+1) y-20 = 0
Cho 4 điểm A( 1 ;2) và B( -1 ; 4) ; C( 2 ;2) ; D( -3 ; 2). Tìm tọa độ giao điểm của 2 đường thẳng AB và CD
Cho đường thẳng d: 3x-4y + 2=0. Có đường thẳng a và b cùng song song với d và cách d một khoảng bằng 1. Hai đường thẳng đó có phương trình là:
Tam giác ABC có đỉnh A(-1; -3) . Phương trình đường cao BB’: 5x+ 3y -25= 0; phương trình đường cao
CC’: 3x+8y -12= 0. Toạ độ đỉnh B là
Phương trình tham số của đường thẳng d qua điểm M( -2 ; 3) và vuông góc với đường thẳng d’ : 3x - 4y +1= 0 là:
Toạ độ hình chiếu của M(4; 1) trên đường thẳng d: x- 2y + 4= 0 là:
Phương trình đường thẳng d qua M( 1;4) và chắn trên hai trục toạ độ những đoạn bằng nhau là
Cho đường thẳng d qua điểm M(1 ;3) và có vectơ chỉ phương Phương trình nào sau đây không phải là phương trình của d?
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và vuông góc nhau ?