Đường tròn (C) có tâm I( -1; 3) và tiếp xúc với đường thẳng d: 3x – 4y + 5= 0 tại điểm H có tọa độ là
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Do đường tròn tiếp xúc với đường thẳng d tại H nên IH và d vuông góc với nhau.
Đường thẳng IH: qua I( -1; 3) và nhận VTCP ( 3; -4) nên có VTPT ( 4;3) nên có phương trình là :
4( x + 1) + 3( y-3) =0 hay 4x+ 3y – 5= 0.
Ta có: IH và d cắt nhau tại H nên tọa độ của H là nghiệm hệ:
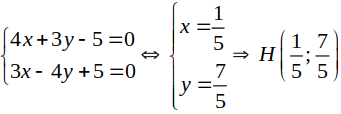
Chọn B.
Tìm giao điểm 2 đường tròn ( C1): x2+ y2- 4= 0 và (C2): x2+ y2- 4x -4y+ 4= 0
Tìm bán kính đường tròn đi qua 3 điểm A(0;4) , B(3;4) ,C(3;0).
Xác định vị trí tương đối giữa 2 đường tròn (C1): x2+ y2= 4 và (C2): (x+ 10) 2+ (y-16)2= 1.
Đường tròn x2+ y2+ 4y = 0 không tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?
Cho đường tròn (C): x2+ y2 + 2x – 6y + 5= 0.Phương trình tiếp tuyến của (C) song song với đường thẳng (a) :
x+ 2y -15 = 0 là
Đường tròn (C): (x-2) 2+ (y-1) 2 = 25 không cắt đường thẳng nào trong các đường thẳng sau đây?
Tọa độ giao điểm của đường tròn (C): x2+ y2 – 2x -2y +1= 0 và đường thẳng
Cho đường tròn (C) : (x-3) 2+ (y-1)2 =10. Phương trình tiếp tuyến của (C) tại điểm A( 4;4) là
Đường tròn x2+ y2 - 2x -2y -23= 0 cắt đường thẳng x+ y -2= 0 theo một dây cung có độ dài bằng bao nhiêu?
Với những giá trị nào của m thì đường thẳng ∆: 3x + 4y + 3= 0 tiếp xúc với đường tròn (C) : (x-m) 2+ y2 = 9
Với những giá trị nào của m thì đường thẳng ∆: 4x+ 3y + m= 0 tiếp xúc với đường tròn (C): x2+ y2- 9= 0.
Cho đường tròn (C): x2+ y2 – 3x – y = 0 . Phương trình tiếp tuyến của (C) tại M( 1; -1) là:
Cho elip có phương trình: Khi đó tọa độ tiêu điểm của elip là.