Xác định a để hàm số fx=a2x−2x+2−2 khi x<2 1−ax khi x≥2 liên tục trên ℝ.

Hàm số xác định trên ℝ Với x < 2 => hàm số liên tục Với x > 2 => hàm số liên tục Với x = 2, ta có limx→2+f(x)=limx→2+(1−a)x=2(1−a)=f(2) limx→2−f(x)=limx→2−a2(x−2)x+2−2=limx→2−a2(x+2+2)=4a2 Hàm số liên tục trên ℝ⇔ hàm số liên tục tại x = 2 ⇔limx→2−f(x)=limx→2+f(x)⇔4a2=2(1−a)⇔a=−1,a=12. Vậy a = -1, a = 12

Câu hỏi:

01/07/2022 56

Xác định a để hàm số $f (x) = \{\begin{matrix} \frac{a^{2} (x - 2)}{\sqrt{x + 2} - 2} khi x < 2 \\ (1 - a) x khi x \geq 2 \end{matrix}$ liên tục trên $ℝ$ .

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

Hàm số xác định trên $ℝ$

Với x < 2 => hàm số liên tục

Với x > 2 => hàm số liên tục

Với x = 2, ta có $\lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{+}} (1 - a) x$ $= 2 (1 - a) = f (2)$

$\lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{-}} \frac{a^{2} (x - 2)}{\sqrt{x + 2} - 2}$ $= \lim_{x \to 2^{-}} a^{2} (\sqrt{x + 2} + 2)$ $= 4 a^{2}$

Hàm số liên tục trên $ℝ \Leftrightarrow$ hàm số liên tục tại x = 2

$\Leftrightarrow \lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{+}} f (x)$ $\Leftrightarrow 4 a^{2} = 2 (1 - a)$ $\Leftrightarrow a = - 1, a = \frac{1}{2}$ .

Vậy a = -1, a = $\frac{1}{2}$

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

$\lim_{x \to 1} (2 x + 1)$ bằng

Xem đáp án » 01/07/2022 169

Câu 2:

$\lim 2^{n}$ bằng

Xem đáp án » 01/07/2022 147

Câu 3:

Cho dãy số $(u_{n})$ thỏa mãn $\lim (u_{n} - 2) = 0$ . Giá trị của $\lim u_{n}$ bằng

Xem đáp án » 01/07/2022 108

Câu 4:

Cho hai dãy số $(u_{n}), (v_{n})$ thỏa mãn $\lim u_{n} = 4$ và $\lim v_{n} = 2 .$ Giá trị của $\lim (u_{n} + v_{n})$ bằng

Xem đáp án » 01/07/2022 108

Câu 5:

Hàm số nào dưới đây liên tục trên $ℝ$ ?

Xem đáp án » 01/07/2022 104

Câu 6:

Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt $\vec{x} = \vec{AB}$ ; $\vec{y} = \vec{AC}$ ; $\vec{z} = \vec{AD}$ . Khẳng định nào sau đây đúng?

Xem đáp án » 01/07/2022 98

Câu 7:

Cho hai hàm số $f (x), g (x)$ thỏa mãn $\lim_{x \to 1} f (x) = 3$ và $\lim_{x \to 1} g (x) = 2 .$ Giá trị của $\lim_{x \to 1} [f (x) + g (x)]$ bằng

Xem đáp án » 01/07/2022 95

Câu 8:

Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc $\hat{(IJ, CD)}$ bằng:

Xem đáp án » 01/07/2022 91

Câu 9:

Cho hình lập phương $ABCD . A^{'} B^{'} C^{'} D^{'}$ . Gọi M, N, P lần lượt là trung điểm của các cạnh $AB, AD, C^{'} D^{'}$ .

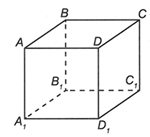
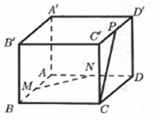
Cosin của góc giữa hai đường thẳng MN, CP bằng

Xem đáp án » 01/07/2022 84

Câu 10:

$\lim_{x \to + \infty} \frac{x - 2}{x + 3}$ bằng

Xem đáp án » 01/07/2022 83

Câu 11:

Cho dãy số $(u_{n})$ thỏa mãn $\lim u_{n} = 5 .$ Giá trị của $\lim (u_{n} - 2)$ bằng

Xem đáp án » 01/07/2022 82

Câu 12:

Cho hình lập phương $ABBC . A_{1} B_{1} C_{1} D_{1}$ (tham khảo hình vẽ).

Góc giữa đường thẳng AD và ${BB}_{1}$ bằng:

Xem đáp án » 01/07/2022 82

Câu 13:

Cho hai dãy số $(u_{n}), (v_{n})$ thỏa mãn $\lim u_{n} = 2$ và $\lim v_{n} = 3 .$ Giá trị của $\lim (u_{n} . v_{n})$ bằng

Xem đáp án » 01/07/2022 81

Câu 14:

$\lim (n + 2)$ bằng

Xem đáp án » 01/07/2022 79

Câu 15:

$\lim \frac{1}{n + 3}$ bằng

Xem đáp án » 01/07/2022 79

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản

7 đề 39419 lượt thi Thi thử
93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải

5 đề 29608 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn nâng cao

4 đề 24641 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn cơ bản

4 đề 23598 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao

6 đề 19425 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác nâng cao

6 đề 18111 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác cơ bản

5 đề 18022 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm cơ bản

6 đề 17390 lượt thi Thi thử
Trắc nghiệm Hàm số lượng giác có đáp án

2 đề 15716 lượt thi Thi thử
Bài tập Lượng Giác cơ bản , nâng cao có lời giải

13 đề 11800 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Cho hàm số $f (x) = {(3 x^{2} - 2 x - 1)}^{9}$ . Tính đạo hàm cấp 6 của hàm số tại điểm x=0.

230 21/10/2022 Xem đáp án
Cho hàm số $y = \sin \frac{x}{2}$ . Đạo hàm $y^{(n)}$ là

157 21/10/2022 Xem đáp án
Cho hàm số y=sin3x.cosx-sin2x . Giá trị của $y^{(10)} (\frac{π}{3})$ gần nhất với số nào dưới đây?

236 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=sin2x là

145 21/10/2022 Xem đáp án
Đạo hàm cấp 2021 của hàm số f(x)=cos(x+a) là

158 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{x}{x^{2} + 5 x + 6}$ là

163 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \frac{2 x + 1}{x^{2} - 3 x + 2}$ là

203 21/10/2022 Xem đáp án
Đạo hàm cấp $n$ của hàm số $y = \sqrt{2 x + 1}$ là

207 21/10/2022 Xem đáp án
Đạo hàm cấp n của hàm số y=cos2x là

240 21/10/2022 Xem đáp án
Cho hàm số $y = \sin^{2} 2 x$ . Giá trị của biểu thức $y^{(3)} + {y^{'}}^{'} + 16 y^{'} + 16 y - 8$ là

142 21/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Xác định a để hàm số fx=a2x−2x+2−2 khi x<2 1−ax khi x≥2 liên tục trên ℝ.

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

limx→12x+1 bằng

Câu 2:

lim 2n bằng

Câu 3:

Cho dãy số un thỏa mãn limun−2=0. Giá trị của lim un bằng

Câu 4:

Cho hai dãy số un,vn thỏa mãn lim un=4 và lim vn=2. Giá trị của limun+vn bằng

Câu 5:

Hàm số nào dưới đây liên tục trên ℝ ?

Câu 6:

Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt x→=AB→; y→=AC→; z→=AD→. Khẳng định nào sau đây đúng?

Câu 7:

Xác định a để hàm số $f (x) = \{\begin{matrix} \frac{a^{2} (x - 2)}{\sqrt{x + 2} - 2} khi x < 2 \\ (1 - a) x khi x \geq 2 \end{matrix}$ liên tục trên $ℝ$ .

$\lim_{x \to 1} (2 x + 1)$ bằng

$\lim 2^{n}$ bằng

Cho dãy số $(u_{n})$ thỏa mãn $\lim (u_{n} - 2) = 0$ . Giá trị của $\lim u_{n}$ bằng

Cho hai dãy số $(u_{n}), (v_{n})$ thỏa mãn $\lim u_{n} = 4$ và $\lim v_{n} = 2 .$ Giá trị của $\lim (u_{n} + v_{n})$ bằng

Hàm số nào dưới đây liên tục trên $ℝ$ ?

Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt $\vec{x} = \vec{AB}$ ; $\vec{y} = \vec{AC}$ ; $\vec{z} = \vec{AD}$ . Khẳng định nào sau đây đúng?