39 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 2)

Câu 1:

(u_{n})

thỏa mãn

\lim (u_{n} - 2) = 0

. Giá trị của

\lim u_{n}

bằng

A. -2

B. 2

C. 1

D. 0

Xem đáp án

Chọn B

Ta có: $\lim (u_{n} - 2) = 0 \Leftrightarrow \lim u_{n} = 2$

Câu 2:

$\lim (n + 2)$ bằng

A. $+ \infty .$

B. $- \infty .$

C. 1

D. 2

Xem đáp án

Chọn A

Ta có:

$\lim (n + 2) = \lim n (1 + \frac{2}{n}) = \lim n . \lim (1 + \frac{2}{n}) = + \infty$

Câu 3:

Cho hai dãy số

(u_{n}), (v_{n})

thỏa mãn

\lim u_{n} = 4

và

\lim v_{n} = 2 .

Giá trị của

\lim (u_{n} + v_{n})

bằng

A. 2

B. 8

C. -2

D. 6

Xem đáp án

Chọn D

Ta có:

$lim (u_{n} + v_{n}) = {limu}_{n} + {limv}_{n} = 4 + 2 = 6$

Câu 4:

$\lim \frac{1}{n + 3}$ bằng

A. 1

B. $+ \infty .$

C. 0

D. $\frac{1}{3} .$

Xem đáp án

Chọn C

Ta có:

\lim \frac{1}{n + 3} = \lim \frac{\frac{1}{n}}{1 + \frac{3}{n}} = \frac{\lim \frac{1}{n}}{1 + \lim \frac{3}{n}} = 0

Câu 5:

$\lim 2^{n}$ bằng

A. $+ \infty .$

B. $- \infty .$

C. 2

D. 0

Xem đáp án

Chọn A

Câu 6:

Cho hai dãy số

(u_{n}), (v_{n})

thỏa mãn

\lim u_{n} = 2

và

\lim v_{n} = 3 .

Giá trị của

\lim (u_{n} . v_{n})

bằng

A. 6

B. 5

C. 1

D. -1

Xem đáp án

Chọn A

Ta có:

\lim (u_{n} . v_{n}) = \lim u_{n} . \lim v_{n} = 2 .3 = 6

Câu 7:

Cho dãy số

(u_{n})

thỏa mãn

\lim u_{n} = 5 .

Giá trị của

\lim (u_{n} - 2)

bằng

A. -3

B. 3

C. 10

D. -10

Xem đáp án

Chọn B

Ta có:

\lim (u_{n} - 2) = \lim u_{n} - 2 = 5 - 2 = 3

Câu 8:

Cho hai hàm số

f (x), g (x)

thỏa mãn

\lim_{x \to 1} f (x) = 3

và

\lim_{x \to 1} g (x) = 2 .

Giá trị của

\lim_{x \to 1} [f (x) + g (x)]

bằng

A. 5.

B. 6.

C. 1.

D. -1.

Xem đáp án

Chọn A

Ta có:

\lim_{x \to 1} [f (x) + g (x)] = \lim_{x \to 1} f (x) + \lim_{x \to 1} g (x) = 3 + 2 = 5

Câu 9:

Cho hàm số $f (x)$ thỏa mãn $\lim_{x \to 1^{+}} f (x) = 2$ và $\lim_{x \to 1^{-}} f (x) = 2.$ Giá trị của $\lim_{x \to 1} f (x)$ bằng

A. 2.

B. 1.

C. 4.

D. 0.

Xem đáp án

Chọn A

Ta có:

\lim_{x \to 1^{+}} f (x) = \lim_{x \to 1^{-}} f (x) = 2

Câu 10:

$\lim_{x \to 1} (2 x + 1)$ bằng

$A . 3 .$

$B . 1 .$

$C . + \infty .$

$D . - \infty .$

Xem đáp án

Chọn A

Câu 11:

$\lim_{x \to + \infty} \frac{x - 2}{x + 3}$ bằng

A. $- \frac{2}{3}$

B. 1

C. 2

D. -3

Xem đáp án

Chọn B

Chia cả tử và mẫu cho x , ta có

\lim_{x \to + \infty} \frac{x - 2}{x + 3} = \lim_{x \to + \infty} \frac{1 - \frac{2}{x}}{1 + \frac{3}{x}} = 1

Câu 12:

Giá trị của

\lim_{x \to 1} (2 x^{2} - 3 x + 1)

bằng

A. 2

B. 1

C. $+ \infty .$

D. 0

Xem đáp án

Chọn D

Ta có:

\lim_{x \to 1} (2 x^{2} - 3 x + 1) = 0

Câu 13:

Tính giới hạn

L = \lim_{x \to 3} \frac{x - 3}{x + 3}

A. $L = - \infty .$

B. L = 0

C. $L = + \infty .$

D. L = 1

Xem đáp án

Chọn B

Ta có

L= \lim_{x \to 3} \frac{x - 3}{x + 3} = 0

Câu 14:

$\lim_{x \to - \infty} \frac{4 x + 1}{- x + 1}$ bằng

A. 2.

B. 4.

C. -1.

D. -4.

Xem đáp án

Chọn D

\lim_{x \to - \infty} \frac{4 x + 1}{- x + 1} = \lim_{x \to - \infty} \frac{4 + \frac{1}{x}}{- 1 + \frac{1}{x}} = - 4

Câu 15:

Tính giới hạn $\lim_{x \to - \infty} (2 x^{3} - x^{2} + 1)$

A. $+ \infty .$

B. $- \infty$ .

C. 2

D. 0

Xem đáp án

Chọn B

Ta có

\lim_{x \to - \infty} (2 x^{3} - x^{2} + 1) = \lim_{x \to - \infty} x^{3} (2 - \frac{1}{x^{2}} + \frac{1}{x^{3}}) = - \infty

Câu 16:

Tính $L = \lim_{x \to - \infty} \frac{2 x + 1}{x + 1}$

A. L = -2

B. L = -1

C. $L = - \frac{1}{2}$

D. L = 2

Xem đáp án

Chọn D

Ta có

L = \lim_{x \to - \infty} \frac{2 x + 1}{x + 1} = \lim_{x \to - \infty} \frac{x (2 + \frac{1}{x})}{x (1 + \frac{1}{x})}

= \lim_{x \to - \infty} \frac{2 + \frac{1}{x}}{1 + \frac{1}{x}} = \frac{2 + 0}{1 + 0} = 2

Câu 17:

Giới hạn

\lim_{x \to - \infty} (3 x^{3} + 5 x^{2} - 9 \sqrt{2} x - 2017)

bằng

A. $- \infty$

B. 3

C. -3

D. $+ \infty$

Xem đáp án

Chọn A

$\lim_{x \to - \infty} (3 x^{3} + 5 x^{2} - 9 \sqrt{2} x - 2017) = \lim_{x \to - \infty} x^{3} (3 + 5 \frac{1}{x} - 9 \sqrt{2} \frac{1}{x^{2}} - 2017 \frac{1}{x^{3}}) = - \infty$

Câu 18:

Tính $\lim_{x \to + \infty} (\sqrt{x^{2} - 4 x + 2} - x)$

A. -4.

B. -2.

C. 4.

D. 2.

Xem đáp án

Chọn B

\lim_{x \to + \infty} (\sqrt{x^{2} - 4 x + 2} - x) = \lim_{x \to + \infty} \frac{x^{2} - 4 x + 2 - x^{2}}{\sqrt{x^{2} - 4 x + 2} + x} = \lim_{x \to + \infty} \frac{- 4 x + 2}{\sqrt{x^{2} - 4 x + 2} + x} = \lim_{x \to + \infty} \frac{- 4 + \frac{2}{x}}{\sqrt{1 - \frac{4}{x} + \frac{2}{x^{2}}} + 1} = - 2

Câu 19:

Tính $\lim_{x \to 1} \frac{\sqrt{x + 3} - 2}{x - 1}$ bằng

A. $\frac{1}{4}$

B. $+ \infty$

C. $\frac{1}{2}$

D. 1

Xem đáp án

Chọn A

Ta có:

\lim_{x \to 1} \frac{\sqrt{x + 3} - 2}{x - 1} = \lim_{x \to 1} \frac{x + 3 - 4}{(x - 1) (\sqrt{x + 3} + 2)} = \lim_{x \to 1} \frac{1}{\sqrt{x + 3} + 2} = \frac{1}{4}

Câu 20:

Hàm số

y = \frac{2 x - 1}{x + 1}

gián đoạn tại điểm nào dưới đây?

A. x = 2

B. x = -1

C. x = 1

D. x = 0

Xem đáp án

Chọn B

Hàm số $y = \frac{2 x - 1}{x + 1}$ là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định của nó là $(- \infty; - 1)$ và $(- 1; + \infty)$ . Do đó, hàm số $y = \frac{2 x - 1}{x + 1}$ gián đoạn tại điểm $x = - 1$

Câu 21:

Hàm số

y = \frac{2 x - 1}{(x + 1) (x^{2} - 3 x + 2)}

liên tục tại điểm nào dưới đây?

A. x = 2

B. x = -1

C. x = 1

D. x = -3

Xem đáp án

Chọn D

Hàm số $y = \frac{2 x - 1}{(x + 1) (x^{2} - 3 x + 2)}$ là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định của nó là $(- \infty; - 1)$ , $(- 1; 1)$ , $(1; 2)$ và $(- 1; + \infty)$ .

Do đó, hàm số $y = \frac{2 x - 1}{(x + 1) (x^{2} - 3 x + 2)}$ liên tục tại điểm $x = - 3$

Câu 22:

Hàm số

f (x) = \frac{5 x - 1}{x^{2} - 5 x + 6}

liên tục trên khoảng nào dưới đây?

A. $(- \infty; + \infty)$

B. (0;3)

C. (4;6)

D. (2;5)

Xem đáp án

Chọn C

Hàm số $f (x) = \frac{5 x - 1}{x^{2} - 5 x + 6}$ là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xácđịnh của nó là $(- \infty; 2)$ và $(3; + \infty)$ .

Vì $(4; 6) \subset (3; + \infty)$ nên hàm số $f (x) = \frac{5 x - 1}{x^{2} - 5 x + 6}$ liên tục trên khoảng (4;6).

Câu 23:

Cho hàm số

f (x) = \{\begin{matrix} 2 x - 5 khi x \neq - 1 \\ 3 m - 1 khi x = - 1 \end{matrix}

. Giá trị của tham số m để hàm số

f (x)

liên tục tại x = -1 bằng

A. 2

B. -2

C. 1

D. -1

Xem đáp án

Chọn B

Ta có $\lim_{x \to - 1} f (x) = \lim_{x \to - 1} (2 x - 5) = - 7$ và $f (- 1) = 3 m - 1$ .

Điều kiện cần và đủ để hàm số đã cho liên tục tại điểm $x = - 1$ là

$\lim_{x \to - 1} f (x) = f (- 1) \Leftrightarrow - 7 = 3 m - 1$ $\Leftrightarrow m = - 2$ .

Câu 24:

Hàm số nào dưới đây liên tục trên khoảng

(- 2; 3) ?

A. $y = \frac{2 x}{x + 1}$

B. $y = \frac{1 - 2 x}{x - 1}$

C. $y = \frac{2 x + 1}{x - 2}$

D. $y = \frac{2 - x}{x + 3}$

Xem đáp án

Chọn D

Hàm số $y = \frac{2 - x}{x + 3}$ xác định và liên tục trên mỗi khoảng $(- \infty; - 3)$ và $(- 3; + \infty)$ . Ta có $(- 2; 3) \subset (- 3; + \infty)$ nên hàm số $y = \frac{2 - x}{x + 3}$ liên tục trên khoảng $(- 2; 3)$ .

Câu 25:

Hàm số nào dưới đây liên tục trên

ℝ

?

A. $y = \frac{2}{sinx + 1}$

B. $y = \tan 2 x + 5$

C. $y = x^{2} - 2 x + cosx$

D. $y = \frac{3}{cosx}$

Xem đáp án

Chọn C

Hàm số $y = x^{2} - 2 x$ là hàm số đa thức nên liên tục trên $ℝ$ , hàm số $y = cosx$ liên tục trên $ℝ$ . Do đó, hàm số $y = x^{2} - 2 x + cosx$ liên tục trên $ℝ$ .

Câu 26:

Cho hai đường thẳng

a, l

song song với nhau và mặt phẳng

(α)

cắt l. Ảnh của a qua phép chiếu song song lên

(α)

theo phương l là

A. một đường thẳng.

B. một điểm.

C. một tia.

D. một đoạn thẳng.

Xem đáp án

Chọn B

Phép chiếu song song biến đường thẳng song song với phương chiếu thành một điểm.

Câu 27:

Cho hình hộp $ABCD . A' B' C' D'$ . Ta có $\vec{BA} + \vec{BC} + \vec{BB'}$ bằng

A. $\vec{AC'}$

B. $\vec{BC'}$

C. $\vec{BD}$

D. $\vec{BD'}$

Xem đáp án

Chọn D

Theo quy tắc hình hộp ta có $\vec{BA} + \vec{BC} + \vec{BB'} = \vec{BD'}$ .

Câu 28:

Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt

\vec{x} = \vec{AB}

;

\vec{y} = \vec{AC}

;

\vec{z} = \vec{AD}

. Khẳng định nào sau đây đúng?

A. $\vec{AG} = \frac{1}{3} (\vec{x} + \vec{y} + \vec{z})$

B. $\vec{AG} = - \frac{1}{3} (\vec{x} + \vec{y} + \vec{z})$

C. $\vec{AG} = \frac{2}{3} (\vec{x} + \vec{y} + \vec{z})$

D. $\vec{AG} = - \frac{2}{3} (\vec{x} + \vec{y} + \vec{z})$

Xem đáp án

Chọn A

Vì G là trọng tâm của tam giác BCD nên ta có $\vec{AB} + \vec{AC} + \vec{AD} = 3 \vec{AG}$ .

Suy ra $\vec{AG} = \frac{1}{3} (\vec{x} + \vec{y} + \vec{z}) .$

Câu 29:

Cho tứ diện ABCD. Đặt

\vec{AB} = \vec{a}, \vec{AC} = \vec{b}, \vec{AD} = \vec{c}

. Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?

A. $\vec{DM} = \frac{1}{2} (\vec{a} + \vec{b} - 2 \vec{c})$

B. $\vec{DM} = \frac{1}{2} (- 2 \vec{a} + \vec{b} + \vec{c})$

C. $\vec{DM} = \frac{1}{2} (\vec{a} - 2 \vec{b} + \vec{c})$

D. $\vec{DM} = \frac{1}{2} (\vec{a} + 2 \vec{b} - \vec{c})$

Xem đáp án

Chọn A

Ta có

$\vec{DM} = \vec{AM} - \vec{AD} = \frac{1}{2} (\vec{AB} + \vec{AC}) - \vec{AD} = \frac{1}{2} (\vec{AB} + \vec{AC} - 2 \vec{AD})$ .

$\Rightarrow \vec{DM} = \frac{1}{2} (\vec{a} + \vec{b} - 2 \vec{c})$ .

Câu 30:

Cho ba vectơ

\vec{a}, \vec{b}, \vec{c}

không đồng phẳng. Xét các vectơ

\vec{x} = 2 \vec{a} - \vec{b};

\vec{y} = - 4 \vec{a} + 2 \vec{b};

\vec{z} = - 3 \vec{b} - 2 \vec{c}

. Chọn khẳng định đúng?

A. Hai vectơ

\vec{y}; \vec{z}

cùng phương.

B. Hai vectơ

\vec{x}; \vec{y}

cùng phương.

C. Hai vectơ $\vec{x}; \vec{z}$ cùng phương.

D. Ba vectơ

\vec{x}; \vec{y}; \vec{z}

đồng phẳng.

Xem đáp án

Chọn B

+ Nhận thấy: $\vec{y} = - 2 (2 \vec{a} - \vec{b}) = - 2 \vec{x}$ nên hai vectơ $\vec{x}; \vec{y}$ cùng phương.

Câu 31:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.

B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.

C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.

D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

Xem đáp án

Chọn D

Trong không gian một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

Câu 32:

Cho hình lập phương

ABBC . A_{1} B_{1} C_{1} D_{1}

(tham khảo hình vẽ).

Góc giữa đường thẳng AD và

{BB}_{1}

bằng:

A. $90 °$

B. $30 °$

C. $45 °$

D. $60 °$

Xem đáp án

Chọn A

Câu 33:

Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc

\hat{(IJ, CD)}

bằng:

A. $60 °$

B. $30 °$

C. $45 °$

D. $90 °$

Xem đáp án

Chọn A

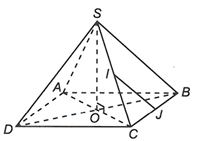
Cho hình chóp S.ABCDcó tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc IJ,CD^ bằng: (ảnh 1)

Từ giả thiết ta có $IJ / / SB$ (do IJ là đường trung bình của $ΔSCB$

và $AB / / CD \Rightarrow (\hat{IJ, CD}) = (\hat{SB, AB}) .$

Mặt khác, ta lại có $ΔSAB$ đều nên $\hat{SBA} = 60^{o} .$

Suy ra $\hat{(SB, AB)} = 60^{o} \Rightarrow \hat{(IJ, CD)} = 60^{o} .$

Câu 34:

Cho hình lập phương

ABCD . A^{'} B^{'} C^{'} D^{'}

. Gọi M, N, P lần lượt là trung điểm của các cạnh

AB, AD, C^{'} D^{'}

.

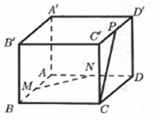
Cosin của góc giữa hai đường thẳng MN, CP bằng

A. $\frac{\sqrt{10}}{5}$

B. $\frac{\sqrt{15}}{5}$

C. $\frac{1}{\sqrt{10}}$

D. $\frac{3}{\sqrt{10}}$

Xem đáp án

Chọn C

Đặt AD = 2a, gọi Q là trung điểm B'C' thì $PQ / / B^{'} D^{'} / / MN$ do đó $\hat{(MN; CP)} = \hat{(PQ; CP)}$

Ta có $PQ = \frac{B^{'} D^{'}}{2} = \frac{2 a \sqrt{2}}{2} = a \sqrt{2}$

$CQ = CP = \sqrt{{(2 a)}^{2} + a^{2}} = a \sqrt{5}$

Do đó $\cos \hat{CPQ} = \frac{{PQ}^{2} + {PC}^{2} - {CQ}^{2}}{2 . PQ . PC} = \frac{1}{\sqrt{10}}$

Vậy $\cos \hat{(MN; CP)} = \frac{1}{\sqrt{10}}$ .

Câu 35:

Cho tứ diện ABCD có AB = AC = AD và

\hat{BAC} = \hat{BAD} = 60 °

,

\hat{CAD} = 90 °

. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ

\vec{AB}

và

\vec{IJ}

?

A. $120 °$

B. $90 °$

C. $45 °$

D. $60 °$

Xem đáp án

Chọn B

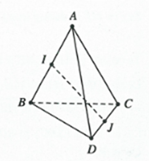
Cho tứ diện ABCD có AB=AC=AD và BAC^=BAD^=60°, CAD^=90°. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→? (ảnh 1)

Xét tam giác ICD có J là trung điểm CD $\Rightarrow \vec{IJ} = \frac{1}{2} (\vec{IC} + \vec{ID})$

Tam giác ABC có $\{\begin{cases} AB = AC \\ \hat{BAC} = 60 ° \end{cases}$ $\Rightarrow ΔABC$ đều $\Rightarrow CI ⊥ AB$

Tương tự ta có $ΔABD$ đều nên $DI ⊥ AB$

Ta có $\vec{IJ} . \vec{AB} = \frac{1}{2} (\vec{IC} + \vec{ID}) . \vec{AB}$ $= \frac{1}{2} \vec{IC} . \vec{AB} + \frac{1}{2} \vec{ID} . \vec{AB} = 0$

$\Rightarrow \vec{IJ} ⊥ \vec{AB} \Rightarrow (\vec{AB}; \vec{IJ}) = 90 °$ .

Câu 36:

Xác định a để hàm số

f (x) = \{\begin{matrix} \frac{a^{2} (x - 2)}{\sqrt{x + 2} - 2} khi x < 2 \\ (1 - a) x khi x \geq 2 \end{matrix}

liên tục trên

ℝ

.

Xem đáp án

Hàm số xác định trên $ℝ$

Với x < 2 => hàm số liên tục

Với x > 2 => hàm số liên tục

Với x = 2, ta có $\lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{+}} (1 - a) x$ $= 2 (1 - a) = f (2)$

$\lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{-}} \frac{a^{2} (x - 2)}{\sqrt{x + 2} - 2}$ $= \lim_{x \to 2^{-}} a^{2} (\sqrt{x + 2} + 2)$ $= 4 a^{2}$

Hàm số liên tục trên $ℝ \Leftrightarrow$ hàm số liên tục tại x = 2

$\Leftrightarrow \lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{+}} f (x)$ $\Leftrightarrow 4 a^{2} = 2 (1 - a)$ $\Leftrightarrow a = - 1, a = \frac{1}{2}$ .

Vậy a = -1, a = $\frac{1}{2}$

Câu 37:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD, biết

AB = CD = a,

MN = \frac{a \sqrt{3}}{2}

. Tính góc giữa hai đường thẳng AB và CD.

Xem đáp án

Cách 1.

Gọi I là trung điểm của AC. Ta có $\{\begin{cases} IM ∥ AB \\ IN ∥ CD \end{cases} \Rightarrow$ $\hat{(AB, CD)} = \hat{(IM, IN)}$

Đặt $\hat{MIN} = α$ , xét tam giác IMN có $IM = \frac{AB}{2} = \frac{a}{2},$ $IN = \frac{CD}{2} = \frac{a}{2},$ $MN = \frac{a \sqrt{3}}{2}$ .

Theo định lí côsin, ta có

$cosα = \frac{{IM}^{2} + {IN}^{2} - {MN}^{2}}{2 IM . IN}$ $= \frac{{(\frac{a}{2})}^{2} + {(\frac{a}{2})}^{2} - {(\frac{a \sqrt{3}}{2})}^{2}}{2 . \frac{a}{2} . \frac{a}{2}}$ $= - \frac{1}{2} < 0$

$\Rightarrow \hat{MIN} = 120^{0}$ suy ra $\hat{(AB, CD)} {=60}^{0}$ .

Cách 2.

$\cos \hat{(AB, CD)} = \cos \hat{(IM, IN)}$ $= \frac{|\vec{IM} . \vec{IN}|}{|\vec{IM}| |\vec{IN}|}$

$\vec{MN} = \vec{IN} - \vec{IM} \Rightarrow$ ${\vec{MN}}^{2} = {(\vec{IN} - \vec{IM})}^{2}$ $= {IM}^{2} + {IN}^{2} - 2 \vec{IN} . \vec{IM}$

$\vec{IN} . \vec{IM} = \frac{{IM}^{2} + {IN}^{2} - {MN}^{2}}{2} = - \frac{a^{2}}{8}$

$\cos \hat{(AB, CD)} = |\cos \hat{(IM, IN)}|$ $= \frac{|\vec{IM} . \vec{IN}|}{|\vec{IM}| |\vec{IN}|} = \frac{1}{2}$

Vậy $\hat{(AB, CD)} {=60}^{0}$ .

Câu 38:

Tìm hai số a, b biết rằng b > 0, a + b = 5 và

\lim_{x \to 0} \frac{\sqrt[3]{ax + 1} - \sqrt{1 - bx}}{x} = 2

.

Xem đáp án

Ta có $\lim_{x \to 0} \frac{\sqrt[3]{ax + 1} - \sqrt{1 - bx}}{x}$ $= \lim_{x \to 0} [\frac{\sqrt[3]{ax + 1} - 1 + 1 - \sqrt{1 - bx}}{x}]$

$= \lim_{x \to 0} \frac{\sqrt[3]{ax + 1} - 1}{x} - \lim_{x \to 0} \frac{\sqrt{1 - bx} - 1}{x}$

$= \lim_{x \to 0} \frac{a}{\sqrt[3]{{(ax + 1)}^{2} + \sqrt[3]{ax + 1} + 1}}$ $+ \lim_{x \to 0} \frac{b}{\sqrt{1 - bx} + 1}$

$= \frac{a}{3} + \frac{b}{2}$

$\Rightarrow \frac{a}{3} + \frac{b}{2} = 2 \Rightarrow 2 a + 3 b = 12$

Do đó ta có hệ

\{\begin{cases} a + b = 5 \\ 2 a + 3 b = 12 \end{cases} \Leftrightarrow \{\begin{cases} a = 3 \\ b = 2 \end{cases}

.

Câu 39:

Tính I =

\lim (\frac{1}{\sqrt{n^{2} + n + 1}} + \frac{1}{\sqrt{n^{2} + n + 2}} + . .. + \frac{1}{\sqrt{n^{2} + 2 n}})

Xem đáp án

Ta có: $\frac{1}{\sqrt{n^{2} + 2 n}} < \frac{1}{\sqrt{n^{2} + n + k}} < \frac{1}{\sqrt{n^{2} + n + 1}},$ $\forall k = 2, 3, . .., n - 1$

$\Rightarrow \frac{n}{\sqrt{n^{2} + 2 n}} < \frac{1}{\sqrt{n^{2} + n + 1}} + \frac{1}{\sqrt{n^{2} + n + 2}}$ $+ . .. + \frac{1}{\sqrt{n^{2} + 2 n}} < \frac{n}{\sqrt{n^{2} + n + 1}}$

Mà $\lim \frac{n}{\sqrt{n^{2} + 2 n}} = \lim \frac{1}{\sqrt{1 + \frac{2}{n}}} = 1$ ; $\lim \frac{n}{\sqrt{n^{2} + n + 1}} = \lim \frac{1}{\sqrt{1 + \frac{1}{n} + \frac{1}{n^{2}}}} = 1$

Vậy I = 1

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương