Giải bởi qa.haylamdo.com
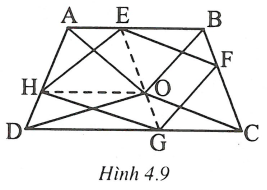
Qua O dựng một đường thẳng song song với BC cắt AB và CD lần lượt tại E và G. Qua O dựng một đường thẳng song song với CD cắt AD tại H.
Qua E dựng một đường thẳng song song với OC cắt BC tại F.
Khi đó tứ giác EFGH thỏa mãn đề bài.
Thật vậy, các tứ giác AEOH, HOGD là những hình thang cân.
=> OA = EH, OD = HG (1)
Tứ giác EFCO là hình bình hành => OC = EF (2)
và OE = CF. Suy ra OG = BF
Vậy tứ giác OBFG là hình bình hành => OB = GF (3)
Từ (1), (2), (3) suy ra tứ giác EFGH thỏa mãn đề bài.
Cho hình bình hành ABCD (AD < AB) . Vẽ ra ngoài hình bình hành tam giác ABM cân tại B và tam giác ADN cân tại D sao cho
a) Chứng minh rằng CM = CN
Cho hình bình hành ABCD. Vẽ ra ngoài hình bình hành các tam giác ABM vuông cân tại A, tam giác BCN vuông cân tại C. Chứng minh rằng tam giác DMN vuông cân.
Cho hình bình hành ABCD và đường thẳng xy không cắt các cạnh của hình bình hành. Qua các đỉnh A, B, C, D vẽ các đường thẳng vuông góc với xy, cắt xy lần lượt tại A', B', C', D'. Chứng minh rằng: AA' + CC' = BB' + DD'
