Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
A.
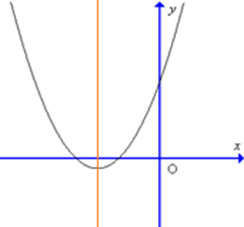
B.
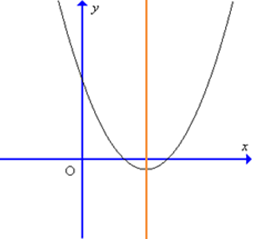
C.
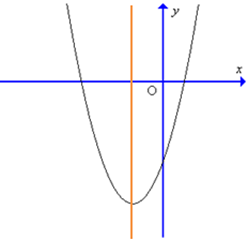
D.
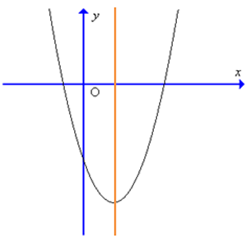
Giải bởi qa.haylamdo.com
Đáp án đúng là: D
Giao điểm của đồ thị với trục tung tại A(0; – 1) nên đồ hàm số cắt trục tung tại điểm có tung độ âm. Do đó chỉ có hình C và hình D thỏa mãn.
Hàm số có trục đối xứng \[x = \frac{3}{8} > 0\]nên trục đối xứng nằm về phần dương của trục Ox.
Do đó hình D là hình vẽ đúng.
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
Cho hàm số y = f(x) có đồ thị như hình sau:
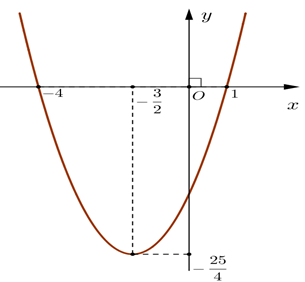
Hàm số đồng biến trên khoảng
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
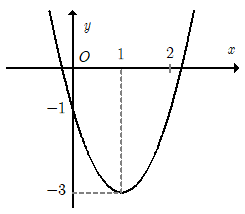
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
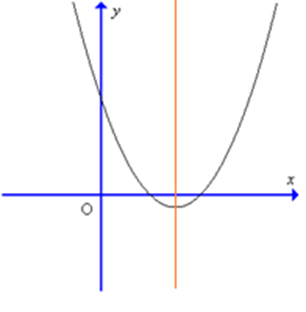
Kết luận nào sau đây đúng về hệ số a, b:
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\). Tính tích P = a.b.
