Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC, SB = SD. Khẳng định nào sau đây là đúng?
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
∙ SA = SC Þ Tam giác SAC cân tại S
Þ SO là đường cao tam giác SAC Þ SO ^ AC (1)
∙ SB = SD Þ Tam giác SBD cân tại S
Þ SO là đường cao tam giác SBD Þ SO ^ BD (2)
Từ (1) và (2) suy ra SO ^ (ABCD).
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là
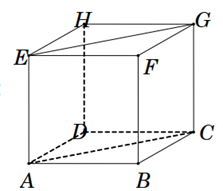
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính d(AB, (EFGH)).
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a. Biết SB vuông góc với mặt đáy, P là trung điểm của cạnh AC.
Chứng minh rằng AC ^ (SBP).
Cho hai hàm số f(x), g(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x)\)= −6 và \(\mathop {\lim }\limits_{x \to 1} g(x)\)= 3. Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) - g(x)} \right]\) bằng:
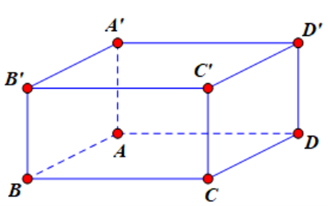
Cho hình lập phương ABCD.A’B’C’D’. Bộ ba vectơ nào sau đây đồng phẳng?
Cho hình chóp S.ABC có SA ^ (ABC).
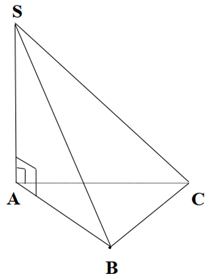
Góc giữa đường thẳng SC và mặt phẳng (ABC) là
Tính các giới hạn sau.
A = lim\(\frac{{2{n^2} - n + 2}}{{3{n^2} + 5n}}\)
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng
Tổng S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ … có giá trị là
