Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên đều bằng . Góc giữa cạnh bên SB và (ABCD) bằng:
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Lời giải
Chọn B.
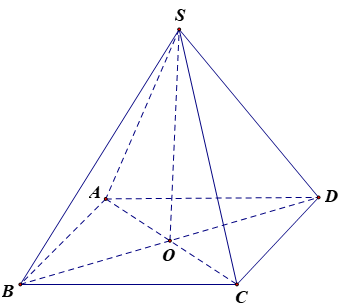
Gọi O là tâm của đáy.
Ta có: cân tại S, SO là trung tuyến nên .
Tương tự .
Vậy , do đó OB là hình chiếu của SB trên (ABCD0.
Suy ra góc giữa cạnh bên SB và (ABCD) bằng (do vuông tại O).
Ta có .
Xét tam giác vuông tại O có .
Vậy góc giữa cạnh bên SB và (ABCD) là .
Cho hình chóp SABC có SA=SC=AB=AC= và BC=2a. Khi đó góc giữa hai đường thẳng AC và SB.
Cho hình chóp ABCD có đáy ABC là tam giác đều cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Biết . Gọi M là điểm thuộc đường cao AH của tam giác ABC. Xét mặt phẳng (P) đi qua M và vuông góc với . Xác định vị trí điểm M để thiết diện của hình chóp cắt bởi mặt phẳng (P) có điện tích lớn nhất. Khi đó bằng:
Cho hình chóp SABC có và . H là hình chiếu vuông góc của A lên SB. Khẳng định nào sau đây là đúng?
Cho hình chóp SABCD có đáy là hình vuông ABCD cạnh bằng a, và SA vuông góc với mặt phẳng đáy ABCD. Gọi là góc giữa SBvà mặt phẳng (SAC). Tính ?