Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA⊥(ABCD) , SA=a√2 . Tính diện tích thiết diện tạo bởi hình chóp SABCD với mặt phẳng (α) đi qua A và vuông góc với SC.
A. S=a2√23
B. S=a2√22
C. S=a2√33
D. S=4a2√22
Giải bởi qa.haylamdo.com
Lời giải
Chọn A.
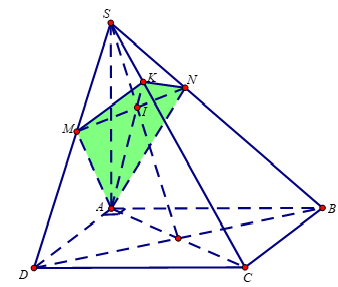
Ta có AM⊥SDAM⊥DC(DC⊥(SAD))}AM⊥SC.
Tương tự AN⊥SC .
Vậy SC⊥(AMN) hay mặt phẳng (AMN) là mặt phẳng thỏa mãn yêu cầu đầu bài.
Gọi SO∩MN={I},AI∩SC={K}. Thiết diện tạo thành là tứ giác AMKN.
Ta có MN⊥AK vậy SAMKN=12MN.AK.
Xét tam giác vuông SAD có 1AM2=1AD2+1AS2⇔AM=a√23.
Tương tự AK=12SC=a.
Mặt khác : SD=a√3, SA2=SM.SD⇒SM=2a2a√3=2a√33.
Tam giác SMN đồng dạng với tam giác SBD ta có MNBD=SMSD⇒MN=BD.SMSD⇒MN=a√2.2a√33a√3=2a√23.
Vậy SAMKN=122a2√23=SAMKN=a2√23.
Cho hình chóp SABC có SA=SB=SC và tam giác ABC vuông tại C Vẽ SH⊥(ABC),H∈(ABC). Khẳng định nào sau đây đúng?
Cho hai đường thẳng phân biệt a,b và mặt phẳng (P), trong đó . Mệnh đề nào sau đây là sai?
Cho tứ diện ABCD Gọi M và P lần lượt là trung điểm AB và CD Đặt Khẳng định nào sau đây đúng?
