Tìm tất cả giá trị của tham số m để phương trình có nghiệm.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Ta có
Phương trình có nghiệm khi và chỉ khi
Vậy với thì phương trình đã cho có nghiệm.
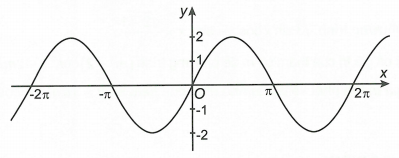
Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau?