Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 1; -1) và đường thẳng . Tọa độ điểm H là hình chiếu vuông góc của M trên đường thẳng D là
A. H(3; -1; 4);
B. H(4; -2; 1);
C. H(-6; 2; 7);
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: A
Ta có:
Phương trình mặt phẳng (P) đi qua M(2; 1; -1) và vuông góc với đường thẳng D nên nhận làm véc-tơ pháp tuyến
(P): -3(x - 2) + (y - 1) + (z + 1) = 0
Û -3x + y + z + 6 = 0
H là hình chiếu vuông góc của M trên đường thẳng D nên là giao của đường thẳng D và mặt phẳng (P) nên ta có
-3(-3 - 3t) + (1 + t) + (6 + t) + 6 = 0
Û 11t + 22 = 0 Û t = -2
Vậy suy ra tọa độ điểm H là H(3; -1; 4).
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; -2) và mặt phẳng (P): 2x + 2y + z + 5 = 0. Mặt cầu (S) có tâm I sao cho mặt phẳng (P) cắt (S) theo giao tuyến là một đường tròn có bán kính . Khi đó phương trình của mặt cầu (S) là
Cho hàm số f (x) có đạo hàm liên tục trên ℝ, f (0) = 0, f '(0) ¹ 0 và thỏa mãn hệ thức f (x).f '(x) + 18x2 = (3x2 + x).f '(x) + (6x + 1).f (x), "x Î ℝ.
Biết , với a, b, c là các số nguyên. Tính giá trị biểu thức P = 2a + 3b + c.
Gọi z1, z2 là hai nghiệm phức của phương trình z2 + 2z + 10 = 0. Giá trị của biểu thức |z1| + |z2| bằng
Diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = f (x), y = g (x) liên tục trên [a; b] và hai đường thẳng x = a, x = b (a < b) được tính theo công thức
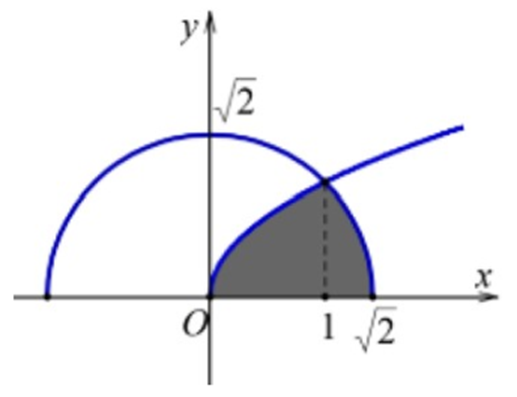
Cho (H) là hình phẳng giới hạn bởi đường cong có phương trình , nửa đường tròn với và trục hoành (phần tô đậm trong hình vẽ). Diện tích của hình (H) bằng
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 0; 3), B(3; 6; -7). Tọa độ trung điểm I của đoạn thẳng AB là
Biết với a, b, c là các số nguyên dương. Tính giá trị của biểu thức P = a + b + c.