50 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 11

Câu 1:

Số phức (3 - 2i)(1 + 2i) bằng

A. 3 + 5i;

B. 1 - 5i;

C. 6 - 4i;

D. 7 + 4i.

Xem đáp án

Đáp án đúng là: D

(3 - 2i)(1 + 2i) = 3 - 2i + 6i - 4i²

= 3 - 2i + 6i + 4 = 7 + 4i.

Câu 2:

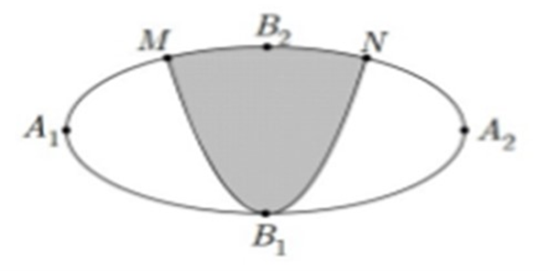
Một biển quảng cáo có dạng hình Elip với bốn đỉnh A₁, A₂, B₁, B₂ như hình vẽ bên. Người ta chia elip bởi parabol có đỉnh B₁, trục đối xứng B₁B₂ và đi qua các điểm M, N. Sau đó sơn phần tô đậm với giá 100 000 đồng/m² và trang trí đèn Led cho phần còn lại với giá 300 000 đồng/m². Tính số tiền để hoàn thành biển quảng cáo trên (làm tròn đến hàng nghìn), biết A₁A₂ = 6m, B₁B₂ = 4m, MN = 4m.

Media VietJack

A. 2 456 000 đồng;

B. 2 015 000 đồng;

C. 3 072 000 đồng;

D. 3 514 000 đồng.

Xem đáp án

Đáp án đúng là: D

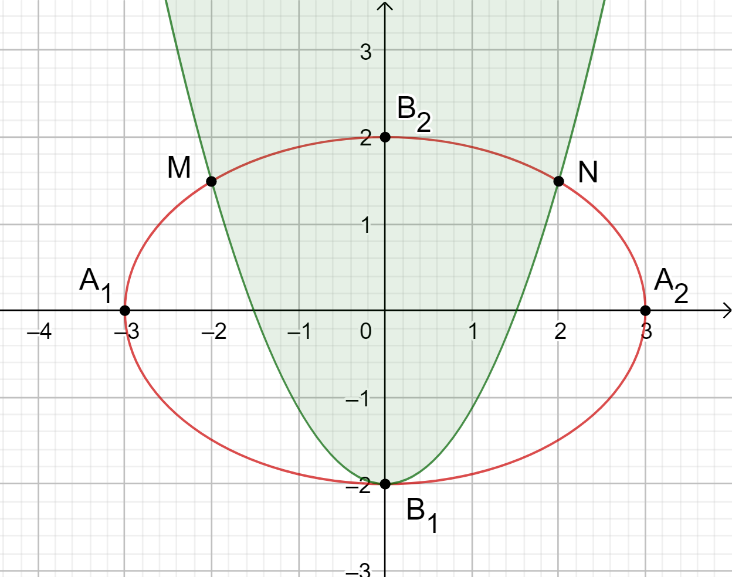
Gán hình dạng của biển quảng cáo vào hệ trục tọa độ Oxy như hình vẽ.

Gọi S là diện tích của hình elip, S₁ là diện tích phần tô đậm và S₂ là diện tích phần còn lại.

Hình elip có A₁A₂ = 6 m, B₁B₂ = 4 m nên suy ra a = 3 m, b = 4 m.

Phương tình elip là: $(E) : \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$

$\Rightarrow y = \pm 2 \sqrt{1 - \frac{x^{2}}{9}}$

Diện tích hình elip là S = pab = 6p.

Thay hoành độ của M, N vào phương tình elip ta suy ra được tọa độ hai điểm

M (- 2; \frac{2 \sqrt{5}}{3}), N (2; \frac{2 \sqrt{5}}{3})

Phương trình parabol có đỉnh B₁, trục đối xứng B₁B₂ và đi qua các điểm M, N có dạng: y = ax² - 2.

Điểm M thuộc parabol nên suy ra $\frac{2 \sqrt{5}}{3} = 4 a - 2 \Leftrightarrow a = \frac{3 + \sqrt{5}}{6}$

Vậy suy ra $y = \frac{3 + \sqrt{5}}{6} x^{2} - 2$

Diện tích phần tô đậm là:

$S_{1} = \int_{- 2}^{2} (2 \sqrt{1 - \frac{x^{2}}{9}} - \frac{3 + \sqrt{5}}{6} x^{2} + 2) d x$

$= \int_{- 2}^{2} (\frac{2}{3} \sqrt{9 - x^{2}} - \frac{3 + \sqrt{5}}{6} x^{2} + 2) d x$

» 10,7055

Þ S₂ = S - S₁ = 6p - S₁

Số tiền để hoàn thành biển quảng cáo trên là

100 000S₁ + 300 000S₂ = 100 000S₁ + 300 000(6p - S₁)

= 3 600 000p - 200 000S₁

» 1 800 000p - 200 000.10,7055

» 3 513 766 (đồng).

Câu 3:

Biết $\int_{0}^{\frac{π}{6}} \frac{x}{\cos^{2} x} d x = \frac{\sqrt{3}}{a} π - \ln b + \frac{1}{2} \ln c$ với a, b, c là các số nguyên dương. Tính giá trị của biểu thức P = a + b + c.

A. P = 9;

B. P = 23;

C. P = 11;

D. P = 27.

Xem đáp án

Đáp án đúng là: B

Đặt $\{\begin{matrix} u = x \Rightarrow d u = d x \\ d v = \frac{1}{\cos^{2} x} d x \Rightarrow v = \tan x \end{matrix}$

Suy ra $\int_{0}^{\frac{π}{6}} \frac{x}{\cos^{2} x} d x = {x \tan x|}_{0}^{\frac{π}{6}} - \int_{0}^{\frac{π}{6}} \tan x d x$

$= {x \tan x|}_{0}^{\frac{π}{6}} - \int_{0}^{\frac{π}{6}} \frac{\sin x}{\cos x} d x = {x \tan x|}_{0}^{\frac{π}{6}} + l {n |\cos x||}_{0}^{\frac{π}{6}}$

$= \frac{π \sqrt{3}}{18} + \ln \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{18} π - \ln 2 + \frac{1}{2} \ln 3$

Mà $\int_{0}^{\frac{π}{6}} \frac{x}{\cos^{2} x} d x = \frac{\sqrt{3}}{a} π - \ln b + \frac{1}{2} \ln c$ nên suy ra a = 18, b = 2, c = 3

Khi đó P = a + b + c = 18 + 2 + 3 = 23.

Câu 4:

Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; -2) và mặt phẳng (P): 2x + 2y + z + 5 = 0. Mặt cầu (S) có tâm I sao cho mặt phẳng (P) cắt (S) theo giao tuyến là một đường tròn có bán kính $r = \sqrt{11}$ . Khi đó phương trình của mặt cầu (S) là

A. (x - 1)² + (y - 2)² + (z + 2)² = 20;

B. (x - 1)² + (y - 2)² + (z + 2)² = 16;

C. (x - 2)² + (y + 2)² + (z - 1)² = 25;

D. (x - 1)² + (y - 2)² + (z + 2)² = 12.

Xem đáp án

Đáp án đúng là: A

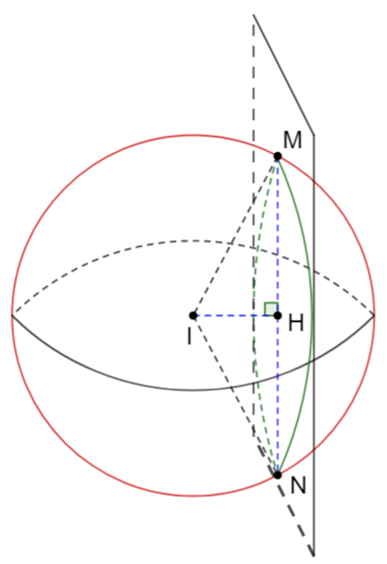
IH là khoảng cách từ I đến mặt phẳng (P) nên:

$I H = d_{I / P} = \frac{|2.1 + 2.2 - 2 + 5|}{\sqrt{2^{2} + 2^{2} + 1^{2}}} = 3$

Mặt cầu (S) có tâm I sao cho mặt phẳng (P) cắt (S) theo giao tuyến là một đường tròn có bán kính $r = \sqrt{11}$ nên suy ra $M H = \sqrt{11}$ .

Áp dụng định lý Py-ta-go vào tam giác IHM vuông tại H nên ta có:

$I M = R = \sqrt{I H^{2} + H M^{2}} = \sqrt{3^{2} + {\sqrt{11}}^{2}} = \sqrt{20}$

Phương trình của mặt cầu (S) có tâm I(1; 2; -2) và có bán kính $R = \sqrt{20}$ là

(S): (x - 1)² + (y - 2)² + (z + 2)² = 20.

Câu 5:

Cho F (x) là một nguyên hàm của hàm số f x) trên [2; 3]. Mệnh đề nào sau đây Đúng?

A. $\int_{2}^{3} f (x) d x = F (3) + F (2);$

B. $\int_{2}^{3} f (x) d x = F (2) - F (3);$

C. $\int_{2}^{3} f (x) d x = F (3) - F (2);$

D. $\int_{2}^{3} f (x) d x = - F (3) - F (2) .$

Xem đáp án

Đáp án đúng là: C

F (x) là một nguyên hàm của hàm số f x) trên [2; 3] nên suy ra

$\int_{2}^{3} f (x) d x = {F (x)|}_{2}^{3} = F (3) - F (2) .$

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 0; 3), B(3; 6; -7). Tọa độ trung điểm I của đoạn thẳng AB là

A. I(2; 3; -5);

B. I(1; 3; -2);

C. I(1; 3; 2);

D. I(4; 6; -10).

Xem đáp án

Đáp án đúng là: B

Gọi I là trung điểm của AB nên suy ra tọa độ trung điểm đoạn thẳng AB là

$\{\begin{matrix} x_{I} = \frac{x_{A} + x_{B}}{2} = \frac{- 1 + 3}{2} = 1 \\ y_{I} = \frac{y_{A} + y_{B}}{2} = \frac{0 + 6}{2} = 3 \\ z_{I} = \frac{z_{A} + z_{B}}{2} = \frac{3 - 7}{2} = - 2 \end{matrix}$

Do đó I(1; 3; -2).

Câu 7:

Tìm các số thực x, y thỏa mãn x + 1 + 4yi = 3 - 2i.

A. x = 2; y = -2;

B. $x = 2; y = \frac{- 1}{2};$

C. $x = \frac{1}{3}; y = 1;$

D. x = 3; y = 2.

Xem đáp án

Đáp án đúng là: B

Ta có: x + 1 + 4yi = 3 - 2i

$\Rightarrow \{\begin{matrix} x + 1 = 3 \\ 4 y = - 2 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 2 \\ y = - \frac{1}{2} \end{matrix}$

Câu 8:

Cho $I = \int_{1}^{2} 2 x {(x^{2} + 1)}^{3} d x$ . Nếu đặt t = x² + 1 thì

A. $I = \int_{1}^{2} t^{3} d t;$

B. $I = \int_{1}^{2} t^{4} d t;$

C. $I = \int_{2}^{5} t^{3} d t;$

D. $I = \int_{2}^{5} 2 t^{3} d t .$

Xem đáp án

Đáp án đúng là: C

Đặt t = x² + 1 Þ dt = 2x dx

Đổi cận:

+) x = 1 Þ y = 2

+) x = 2 Þ y = 5

Nên suy ra

$I = \int_{1}^{2} 2 x {(x^{2} + 1)}^{3} d x = \int_{2}^{5} t^{3} d t .$

Câu 9:

Cho số phức $z = \frac{1 + 5 i}{3 + 2 i}$ . Số phức liên hợp của z là

A. $\bar{z} = 1 - i;$

B. $\bar{z} = 3 - 4 i;$

C. $\bar{z} = 1 + i;$

D. $\bar{z} = 3 + 4 i .$

Xem đáp án

Đáp án đúng là: A

$z = \frac{1 + 5 i}{3 + 2 i} = \frac{(1 + 5 i) (3 - 2 i)}{(3 + 2 i) (3 - 2 i)} = \frac{3 + 15 i - 2 i - 10 i^{2}}{3^{2} + 2^{2}}$

$= \frac{3 + 15 i - 2 i + 10}{3^{2} + 2^{2}} = \frac{13 + 13 i}{13} = 1 + i$

Suy ra số phức liên hợp của z là $\bar{z} = 1 - i .$

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \{\begin{matrix} x = - 1 + 2 t \\ y = 1 + t \\ z = 2 + 3 t \end{matrix}$ và mặt phẳng (P): x - y - z + 3 = 0. Đường thẳng D đi qua M(1; 1; 2) song song với mặt phẳng (P) và vuông góc với đường thẳng d có phương trình là

A. $\frac{x - 1}{2} = \frac{y - 1}{5} = \frac{z + 2}{- 3};$

B. $\frac{x - 1}{2} = \frac{y - 1}{1} = \frac{z + 2}{3};$

C. $\frac{x - 1}{4} = \frac{y - 1}{2} = \frac{z + 2}{3};$

D. $\frac{x + 1}{2} = \frac{y + 1}{1} = \frac{z - 2}{- 2} .$

Xem đáp án

Đáp án đúng là: A

Ta có:

+) $\vec{u_{d}} = (2; 1; 3)$

+) $\vec{n_{P}} = (1; - 1; - 1)$

Đường thẳng D song song với mặt phẳng (P) và vuông góc với đường thẳng d nên $\vec{u_{Δ}}$ đều vuông góc với $\vec{u_{d}}$ và $\vec{n_{P}}$

$\Rightarrow \vec{u_{Δ}} = [\vec{u_{d}}; \vec{n_{P}}] = (|\begin{matrix} 1 & 3 \\ - 1 & - 1 \end{matrix}|; |\begin{matrix} 3 & 2 \\ - 1 & 1 \end{matrix}|; |\begin{matrix} 2 & 1 \\ 1 & - 1 \end{matrix}|)$

= (2; 5; -3)

Đường thẳng D đi qua M(1; 1; 2) và có véc-tơ chỉ phương là (2; 5; -3) có phương trình là $Δ : \frac{x - 1}{2} = \frac{y - 1}{5} = \frac{z + 2}{- 3} .$

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(-1; 1; 6), B(-3; -2; -4), C(1; 2; -1), D(2; -2; 0). Tìm tọa độ điểm M thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất.

A. $M (\frac{1}{2}; 0; \frac{5}{2});$

B. $M (\frac{3}{2}; 0; \frac{- 1}{2});$

C. $M (\frac{5}{3}; \frac{- 2}{3}; \frac{- 1}{3});$

D. M(-1; 10; -3).

Xem đáp án

Đáp án đúng là: B

Ta có: $\vec{C D} = (1; - 4; 1)$ .

Phương trình đường thẳng CD đi qua D vào có véc-tơ chỉ phương là (1; 4; 3)

$C D : \{\begin{matrix} x = 2 + t \\ y = - 2 - 4 t \\ z = t \end{matrix}$

Điểm M thuộc CD nên M(2 + m; -2 - 4m; m).

Để tam giác ABM có chu vi nhỏ nhất thì AM + BM + AB nhỏ nhất.

Mà AB cố định nên AM + BM nhỏ nhất.

Ta có: AM + BM

$= \sqrt{{(m + 3)}^{2} + {(- 4 m - 3)}^{2} + {(m - 6)}^{2}} + \sqrt{{(m + 5)}^{2} + {(- 4 m)}^{2} + {(m + 4)}^{2}}$

$= \sqrt{18 m^{2} + 18 m + 54} + \sqrt{18 m^{2} + 18 m + 41}$

$= \sqrt{18 (m^{2} + m + \frac{1}{4}) + \frac{99}{2}} + \sqrt{18 (m^{2} + m + \frac{1}{4}) + \frac{73}{2}}$

$= \sqrt{18 {(m + \frac{1}{2})}^{2} + \frac{99}{2}} + \sqrt{18 {(m + \frac{1}{2})}^{2} + \frac{73}{2}}$

$\geq \sqrt{\frac{99}{2}} + \sqrt{\frac{73}{2}}$

Dấu “=” xảy ra khi và chỉ khi $m = - \frac{1}{2}$ .

Do đó tọa độ điểm M là $M (\frac{3}{2}; 0; \frac{- 1}{2}) .$

Câu 12:

Cho số phức z = 2 + 3i. Tìm môđun của số phức $w = 1 + 2 \bar{z} + z$

A. $|w| = 7 \sqrt{2};$

B. $|w| = \sqrt{13};$

C. $|w| = 4 \sqrt{3};$

D. $|w| = \sqrt{58} .$

Xem đáp án

Đáp án đúng là: D

+) z = 2 + 3i ; $\Rightarrow \bar{z} = 2 - 3 i$

+) $w = 1 + 2 \bar{z} + z = 1 + 2 (2 - 3 i) + (2 + 3 i)$ = 7 - 3i.

Khi đó môđun của số phức w là:

$|w| = |7 - 3 i| = \sqrt{7^{2} + {(- 3)}^{2}} = \sqrt{58} .$

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - y + 3z - 4 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?

A. $\vec{n} = (2; - 1; 3);$

B. $\vec{n} = (2; 1; 3);$

C. $\vec{n} = (2; - 1; - 4);$

D. $\vec{n} = (- 1; 3; - 4) .$

Xem đáp án

Đáp án đúng là: A

Mặt phẳng (P): 2x - y + 3z - 4 = 0 có vectơ pháp tuyến là $\vec{n} = (2; - 1; 3) .$

Câu 14:

Trong không gian với hệ tọa độ Oxyz, đường thẳng $d : \{\begin{matrix} x = 1 + 2 t \\ y = 2 - 3 t \\ z = - 3 + 4 t \end{matrix}$ đi qua điểm nào dưới đây?

A. M(3; 1; 9);

B. M(1; -4; -3);

C. Q(1; 2; -3);

D. M(3; -4; 9).

Xem đáp án

Đáp án đúng là: C

Lân lượt thử các tọa độ của các điểm trên vào phương trình đường thẳng d ta thấy điểm Q(1; 2; -3) là điểm thuộc d với

$\{\begin{matrix} x_{Q} = 1 + 2 t = 1 \\ y_{Q} = 2 - 3 t = 2 \\ z_{Q} = - 3 + 4 t = - 3 \end{matrix} \Rightarrow t = 0$ (Thỏa mãn)

Câu 15:

Cho số phức z thỏa mãn z(2 + i) = 4 + 7i. Khi đó số phức z là

A. z = 11 - 2i;

B. z = 9 + 4i;

C. z = 3 + 2i;

D. z = -1 + 2i.

Xem đáp án

Đáp án đúng là: C

z(2 + i) = 4 + 7i

$\Rightarrow z = \frac{4 + 7 i}{2 + i} = \frac{(4 + 7 i) (2 - i)}{(2 + i) (2 - i)} = \frac{8 + 14 i - 4 i - 7 i^{2}}{2^{2} + 1^{2}}$

$= \frac{8 + 14 i - 4 i + 7}{5} = \frac{15 + 10 i}{5} = 3 + 2 i .$

Câu 16:

Cho hai số phức z₁ = 1 + 2i, z₂ = 2 - 3i. Tìm số phức w = z₁ - 2z₂.

A. w = 5 + 8i;

B. w = -3 + 8i;

C. w = 3 - i;

D. w = -3 + 4i.

Xem đáp án

Đáp án đúng là: B

w = z₁ - 2z₂ = (1 + 2i) - 2(2 - 3i)

= 1 + 2i - 4 + 6i = -3 + 8i.

Câu 17:

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 3x² - 6x, trục hoành và hai đường thẳng x = 2, x = 4 bằng

A. 27;

B. 16;

C. 12;

D. 20.

Xem đáp án

Đáp án đúng là: D

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 3x² - 6x, trục hoành và hai đường thẳng x = 2, x = 4 bằng

$S = \int_{2}^{4} |3 x^{2} - 6 x| d x = \int_{2}^{4} (3 x^{2} - 6 x) d x$

$= {(x^{3} - 3 x^{2})|}_{2}^{4} = (4^{3} - {3.4}^{2}) - (2^{3} - {3.2}^{2}) = 20.$

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)² + (y + 2)² + (z - 3)² = 12. Gọi (P) là mặt phẳng đi qua hai điểm $A (\frac{- 11}{2}; 0; 0), B (- 3; 0; 5)$ và cắt mặt cầu (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là hình tròn (C) có thể tích lớn nhất. Biết mặt phẳng (P) có phương trình dạng 2x + by + cz + d = 0. Khi đó giá trị biểu thức b² + c² + d² bằng

A. 144;

B. 113;

C. 105;

D. 126.

Xem đáp án

Đáp án đúng là: D

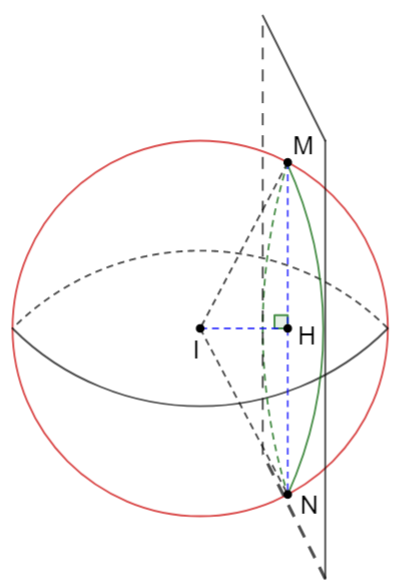
Mặt cầu (S): (x - 1)² + (y + 2)² + (z - 3)² = 12 có tâm I(1; -2; 3) và bán kính $R = 2 \sqrt{3}$

+) $\vec{A B} = (\frac{5}{2}; 0; 5)$

+) Mặt phẳng (P) có phương trình dạng 2x + by + cz + d = 0 có véc-tơ pháp tuyến là

AB thuộc mặt phẳng (P) nên véc-tơ pháp tuyến của (P) vuông góc với

Ta suy ra được hệ phương trình

$\{\begin{matrix} \frac{5}{2} .2 + 0. b + 5 c = 0 \\ 2. (\frac{- 11}{2}) + d = 0 \\ 2. (- 3) + 5 c + d = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} c = - 1 \\ d = 11 \\ 5 c = 6 - d \end{matrix}$

Từ đó suy ra (P) có dạng 2x + by - z + 11 = 0

Khối nón có đỉnh là tâm của (S), đáy là hình tròn (C) có thể tích là

$V = \frac{1}{3} I H . π M H^{2} = \frac{1}{3} I H . π (I M^{2} - I H^{2})$

$= \frac{1}{3} I H . π (12 - I H^{2})$ đạt GTLN khi IH(12 - IH²) đạt GTLN

Ta có:

Với x > 0, xét hàm số f (x) = x(12 - x²) = 12x - x³

Þ f '(x) = 12 - 3x² = 0 Û x² = 4 Þ x = 2 (Do x > 0)

Vẽ được BBT của hàm số f (x) = x(12 - x²) trên (0; +¥)

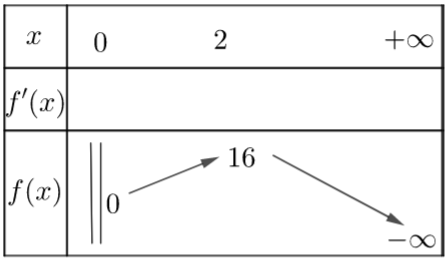
Media VietJack

Dựa vào BBT nên suy ra f (x) đạt GTLN bằng 16 khi x = 2

Nên suy ra IH(12 - IH²) đạt GTLN khi IH = 2

$\Rightarrow I H = d_{I / P} = \frac{|2.1 + b . (- 2) - 3 + 11|}{\sqrt{2^{2} + b^{2} + {(- 1)}^{2}}} = 2$

$\Leftrightarrow \frac{|10 - 2 b|}{\sqrt{b^{2} + 5}} = 2 \Leftrightarrow \frac{|5 - b|}{\sqrt{b^{2} + 5}} = 1$

$|5 - b| = \sqrt{b^{2} + 5}$

Þ |5 - b|² = b² + 5

Û 25 - 10b + b² = b² + 5

Û 10b = 20 Û b = 2

Từ đó suy ra b² + c² + d² = 2² + (-1)² + 11² = 126.

Câu 19:

Cho hàm số f (x) liên tục trên ℝ và $\int_{- 1}^{5} f (x) d x = 15$ . Khi đó giá trị của $\int_{0}^{2} [2022 - f (5 - 3 x)] d x$ bằng

A. 2007;

B. 8083;

C. 4039;

D. 4025.

Xem đáp án

Đáp án đúng là: C

$\int_{0}^{2} [2022 - f (5 - 3 x)] d x = \int_{0}^{2} 2022 d x - \int_{0}^{2} f (5 - 3 x) d x$

Đặt u = 5 - 3x Þ du = -3 dx

Đổi cận:

+) x = 0 Þ u = 5

+) x = 2 Þ u = -1

Nên suy ra

$\int_{0}^{2} 2022 d x - \int_{5}^{- 1} f (u) . (- \frac{1}{3}) d u = \int_{0}^{2} 2022 d x - \frac{1}{3} \int_{- 1}^{5} f (u) d u$

$= {2022 x|}_{0}^{2} - \frac{1}{3} .15 = 2022.2 - \frac{1}{3} .15 = 4039.$

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y - 3z = 0 và đường thẳng $Δ : \frac{x - 2}{- 3} = \frac{y}{1} = \frac{z + 1}{2}$ . Gọi M(a; b; c) là giao điểm của đường thẳng D và mặt phẳng (P). Khi đó tổng 3a + 4b + 5c bằng

A. 6;

B. 9;

C. -27;

D. 13.

Xem đáp án

Đáp án đúng là: A

$Δ : \frac{x - 2}{- 3} = \frac{y}{1} = \frac{z + 1}{2} \Rightarrow \{\begin{matrix} x = 2 - 3 t \\ y = t \\ z = - 1 + t \end{matrix}$

M là điểm thuộc d nên M(2 - 3m; m; -1 + m)

M thuộc mặt phẳng (P) nên suy ra

(2 - 3m) + 2m - 3(-1 + m) = 0

Û 2 - 3m + 2m + 3 - 3m = 0

Û -4m + 5 = 0 $\Leftrightarrow m = \frac{5}{4}$

Từ đó suy ra $M (\frac{- 7}{4}; \frac{5}{4}; \frac{1}{4})$

Vậy suy ra $3 a + 4 b + 5 c = 3. (\frac{- 7}{4}) + 4. \frac{5}{4} + 5. \frac{1}{4} = 1.$

Câu 21:

Họ nguyên hàm của hàm số f (x) = 3^x là

A. $\frac{3^{x}}{x + 1} + C;$

B. 3^x.ln 3 + C;

C. $\frac{3^{x}}{\ln 3} + C;$

D. 3^x + C.

Xem đáp án

Đáp án đúng là: C

Họ nguyên hàm của hàm số f (x) = 3^x là

$F (x) = \int f (x) d x = \int 3^{x} d x = \frac{1}{\ln 3} \int 3^{x} . \ln 3 d x$

$= \frac{3^{x}}{\ln 3} + C .$

Câu 22:

Tìm họ nguyên hàm của hàm số f (x) = 4x³ + 2x

A. F (x) = x⁴ + 2 + C;

B. F (x) = 12x² + 2 + C;

C. F (x) = x² + 4 + C;

D. F (x) = x⁴ + x² + C.

Xem đáp án

Đáp án đúng là: D

Họ nguyên hàm của hàm số f (x) = 4x³ + 2x là

$F (x) = \int f (x) d x = \int (4 x^{3} + 2 x) d x$

= x⁴ + x² + C.

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x² + y² + z² + 2x - 4y + 6z - 2 = 0. Tọa độ tâm I của mặt cầu (S) là

A. I(1; 2; 2);

B. I(-4; 6; 2);

C. I(-1; 2; -3);

D. I(2; -4; 6).

Xem đáp án

Đáp án đúng là: C

Mặt cầu (S): x² + y² + z² + 2x - 4y + 6z - 2 = 0

Û (x² + 2x + 1) + (y² - 4y + 4) + (z² + 6z + 9) = 16

Û (x + 1)² + (y - 2)² + (z + 3)² = 16

Vậy suy ra tọa độ tâm I của mặt cầu (S) là I(-1; 2; -3).

Câu 24:

Cho số phức z thỏa mãn $(- 2 + i) \bar{z} + 3 z = 1 - 3 i$ . Tổng phần thực và phần ảo của số phức $w = z + 2 \bar{z}$ bằng

A. 7;

B. 12;

C. -6;

D. 3.

Xem đáp án

Đáp án đúng là: A

Gọi $z = a + b i \Rightarrow \bar{z} = a - b i$

$(- 2 + i) \bar{z} + 3 z = 1 - 3 i$

Û (-2 + i)(a - bi) + 3(a + bi) = 1 - 3i

Û -2a + ai + 2bi - bi² + 3a + 3bi = 1 - 3i

Û -2a + ai + 2bi + b + 3a + 3bi = 1 - 3i

Û (a + b) + (a + 5b) = 1 - 3i

$\Rightarrow \{\begin{matrix} a + b = 1 \\ a + 5 b = - 3 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 2 \\ b = - 1 \end{matrix}$

Lại có: $w = z + 2 \bar{z} = (a + b i) + 2 (a - b i)$

= 3a - bi = 3.2 - (-1).i = 6 + i

Vậy suy ra tổng phần thực và phần ảo của số phức w là 6 + 1 = 7.

Câu 25:

Họ nguyên hàm của hàm số f (x) = cos 2x là

A. sin 2x + C;

B. $\frac{1}{2} \cos 2 x + C;$

C. -2sin 2x + C;

D. $\frac{1}{2} s i n 2 x + C .$

Xem đáp án

Đáp án đúng là: D

Họ nguyên hàm của hàm số f (x) = cos 2x là

$F (x) = \int f (x) d x = \int \cos 2 x d x = \frac{1}{2} \int 2 \cos 2 x d x$

$= \frac{1}{2} s i n 2 x + C .$

Câu 26:

Cho số phức z thỏa mãn $|z + 3 - 4 i| = \sqrt{2}$ . Biết tập hợp các điểm biểu diễn số phức w = (2 - i)z - 3i + 5 là một đường tròn. Xác định tâm I và bán kính R của đường tròn đó.

A. Đường tròn tâm I(-1; 3), bán kính $R = 3 \sqrt{2};$

B. Đường tròn tâm I(-3; -8), bán kính $R = \sqrt{10};$

C. Đường tròn tâm I(3; 8), bán kính $R = \sqrt{10};$

D. Đường tròn tâm I(1; -3), bán kính

R = 3 \sqrt{2};

Xem đáp án

Đáp án đúng là: C

w = (2 - i)z - 3i + 5

$\Rightarrow \frac{u - 5 + 3 i}{2 - i} = z \Leftrightarrow \frac{u - 5 + 3 i}{2 - i} + 3 - 4 i = z + 3 - 4 i$

$\Leftrightarrow \frac{u - 5 + 3 i + 6 - 8 i - 3 i + 4 i^{2}}{2 - i} = z + 3 - 4 i$

$\Leftrightarrow \frac{u - 5 + 3 i + 6 - 8 i - 3 i - 4}{2 - i} = z + 3 - 4 i$

$\Leftrightarrow \frac{u - 3 - 8 i}{2 - i} = z + 3 - 4 i$

Lấy môđun hai vế ta có

$|\frac{u - 3 - 8 i}{2 - i}| = |z + 3 - 4 i|$

$\Leftrightarrow \frac{|u - 3 - 8 i|}{|2 - i|} = |z + 3 - 4 i|$

$\Leftrightarrow \frac{|u - 3 - 8 i|}{\sqrt{5}} = \sqrt{2}$

$\Leftrightarrow |u - 3 - 8 i| = \sqrt{10}$

Vậy suy ra tập hợp các điểm biểu diễn số phức w = (2 - i)z - 3i + 5 là một đường tròn có tâm I(3; 8) và bán kính $R = \sqrt{10}$ .

Câu 27:

Cho hình phẳng (H) giới hạn bởi đường cong $y = \sqrt{2 x}$ , trục hoành và các đường thẳng x = 1, x = 2. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng

A. 7;

B. 3p;

C. 7p;

D. 3.

Xem đáp án

Đáp án đúng là: B

Hình phẳng (H) giới hạn bởi đường cong $y = \sqrt{2 x}$ , trục hoành và các đường thẳng x = 1, x = 2. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng

$\int_{1}^{2} {\sqrt{2 x}}^{2} d x = \int_{1}^{2} 2 x d x = {x^{2}|}_{1}^{2} = 2^{2} - 1^{2} = 3.$

Câu 28:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{2} = \frac{y + 3}{4} = \frac{z - 1}{3}$ . Vectơ nào dưới đây là một vectơ chỉ phương của d?

A. $\vec{u_{2}} = (1; - 3; 1);$

B. $\vec{u_{1}} = (3; 4; 2);$

C. $\vec{u_{4}} = (3; 1; 1);$

D. $\vec{u_{3}} = (2; 4; 3) .$

Xem đáp án

Đáp án đúng là: D

Đường thẳng $d : \frac{x - 1}{2} = \frac{y + 3}{4} = \frac{z - 1}{3}$ có vectơ chỉ phương là $\vec{u_{3}} = (2; 4; 3) .$

Câu 29:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 1; -1) và đường thẳng $Δ : \{\begin{matrix} x = - 3 - 3 t \\ y = 1 + t \\ z = 6 + t \end{matrix}$ . Tọa độ điểm H là hình chiếu vuông góc của M trên đường thẳng D là

A. H(3; -1; 4);

B. H(4; -2; 1);

C. H(-6; 2; 7);

D. H(6; -2; 3).

Xem đáp án

Đáp án đúng là: A

Ta có: $\vec{u_{Δ}} = (- 3; 1; 1)$

Phương trình mặt phẳng (P) đi qua M(2; 1; -1) và vuông góc với đường thẳng D nên nhận $\vec{u_{Δ}} = (- 3; 1; 1)$ làm véc-tơ pháp tuyến

(P): -3(x - 2) + (y - 1) + (z + 1) = 0

Û -3x + y + z + 6 = 0

H là hình chiếu vuông góc của M trên đường thẳng D nên là giao của đường thẳng D và mặt phẳng (P) nên ta có

-3(-3 - 3t) + (1 + t) + (6 + t) + 6 = 0

Û 11t + 22 = 0 Û t = -2

Vậy suy ra tọa độ điểm H là H(3; -1; 4).

Câu 30:

Cho hàm số f (x) liên tục trên ℝ. Gọi S là diện tích miền hình phẳng được gạch chéo trong hình vẽ bên. Mệnh đề nào dưới đây là Đúng?

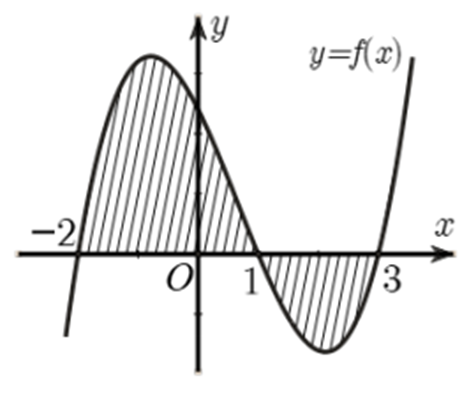
Media VietJack

A. $S = - \int_{- 2}^{3} f (x) d x;$

B. $S = \int_{- 2}^{1} f (x) d x + \int_{1}^{3} f (x) d x;$

C. $S = \int_{- 2}^{1} f (x) d x - \int_{1}^{3} f (x) d x;$

D. $S = \int_{- 2}^{3} f (x) d x .$

Xem đáp án

Đáp án đúng là: C

Diện tích miền hình phẳng được gạch chéo trong hình vẽ bên là

$S = \int_{- 2}^{3} |f (x)| d x = \int_{- 2}^{1} |f (x)| d x + \int_{1}^{3} |f (x)| d x$

$= \int_{- 2}^{1} f (x) d x - \int_{1}^{3} f (x) d x .$

Câu 31:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng D vuông góc với mặt phẳng (a): 3x + 5y - z - 2 = 0. Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng D?

A. $\vec{u_{2}} = (5; - 1; - 2);$

B. $\vec{u_{1}} = (3; 5; - 2);$

C. $\vec{u_{4}} = (3; - 1; - 2);$

D. $\vec{u_{3}} = (3; 5; - 1) .$

Xem đáp án

Đáp án đúng là: D

Mặt phẳng (a): 3x + 5y - z - 2 = 0 nên có véc-tơ pháp tuyến là $\vec{n_{P}} = (3; 5; - 1)$

Đường thẳng D vuông góc với mặt phẳng (a) nên nhận $\vec{n_{P}} = (3; 5; - 1)$ làm véc-tơ chỉ phương

Vậy suy ra véc-tơ chỉ phương của đường thẳng D là $\vec{u_{3}} = (3; 5; - 1) .$

Câu 32:

Nghiệm của phương trình z² - 4z + 5 = 0 trên tập số phức là

A. z = 4 ± 3i;

B. z = 1 ± 2i;

C. z = 2 ± i;

D. z = 4 ± 4i.

Xem đáp án

Đáp án đúng là: C

z² - 4z + 5 = 0

Û z² - 4z + 4 = -1

Û (z - 2)² = i²

$[\begin{matrix} z - 2 = i \\ z - 2 = - i \end{matrix} \Leftrightarrow [\begin{matrix} z = 2 + i \\ z = 2 - i \end{matrix}$

Vậy tập nghiệm phức của phương trình z² - 4z + 5 = 0 trên tập số phức là

z = 2 ± i.

Câu 33:

Các căn bậc hai của số thực -13 là

A. ±13i;

B. $\pm i \sqrt{13};$

C. $- \sqrt{13};$

D. $\sqrt{13} .$

Xem đáp án

Đáp án đúng là: B

căn bậc hai của số thực -13 = 13i² là

$\sqrt{13 i^{2}} = \pm i \sqrt{13} .$

Câu 34:

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng (Oxy)?

A. z = 0;

B. x = 0;

C. y = 0;

D. x - y = 0.

Xem đáp án

Đáp án đúng là: A

Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (Oxy) là z = 0.

Câu 35:

Cho hai số phức z, w thỏa mãn

|\frac{z - i}{z + 2 - 3 i}| = 1

và

|\frac{w + i}{w - 1 + i}| = \sqrt{2}

. Tìm phần ảo của số phức 2z + 3w khi |z - w| đạt giá trị nhỏ nhất

A. 6;

B. -2;

C. 4;

D. 9.

Xem đáp án

Đáp án đúng là: C

+) $|\frac{z - i}{z + 2 - 3 i}| = 1$

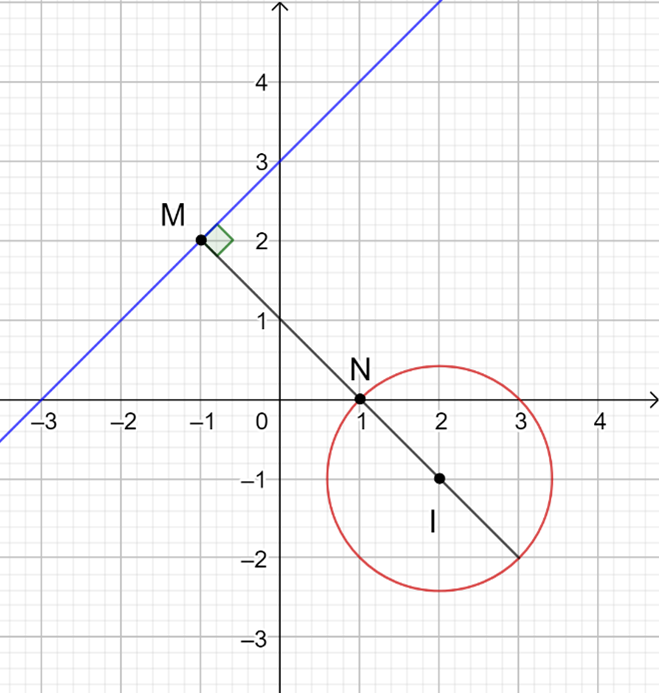
Þ |z - i| = |z + 2 - 3i|

Þ x² + (y - 1)² = (x + 2)² + (y - 3)²

Û x² + y² - 2y + 1 = x² + 4x + 4 + y² - 6y + 9

Û 4x - 4y = - 12 Û y = x + 3

Û D: x - y + 3 = 0

M(x; y) là điểm biểu diễn của số phức z và thuộc đường thẳng y = x + 3

+) $|\frac{w + i}{w - 1 + i}| = \sqrt{2}$

Þ a² + (b + 1)² = 2(a - 1)² + 2(b + 1)²

Û 2(a - 1)² + (b + 1)² - a² = 0

Û 2a² - 4a + 2 + (b + 1)² - a² = 0

Û (a² - 4a + 4) + (b + 1)² = 2

Û (C): (a - 2)² + (b + 1)² = 2

N(a; b) là điểm biểu diễn của số phức w và thuộc đường tròn tâm I(2; -1) và có bán kính $R = \sqrt{2}$

Ta có: |z - w| = MN đạt GTNN

Vậy suy ra MN đi qua tâm I và N gần M nhất

+) $\vec{n_{Δ}} = (1; - 1) \Rightarrow \vec{n_{M N}} = (1; 1)$

Phương trình đường thẳng MN đi qua I(2; -1) và có véc-tơ pháp tuyến là $\vec{n_{M N}} = (1; 1)$

MN: x - 2 + y + 1 = 0

Û x + y - 1 = 0

+) M là giao của đường thẳng D và MN nên ta có tọa độ điểm M thỏa mãn

$\{\begin{matrix} x + y - 1 = 0 \\ x - y + 3 = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + y = 1 \\ x - y = - 3 \end{matrix} \Leftrightarrow \{\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$

Vậy suy ra M(-1; 2) Þ z = -1 + 2i

+) N là giao của đường tròn (C) và MN nên ta có tọa độ điểm N thỏa mãn

$\{\begin{matrix} a + b - 1 = 0 \\ {(a - 2)}^{2} + {(b + 1)}^{2} = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} b = 1 - a \\ {(a - 2)}^{2} + {(b + 1)}^{2} = 2 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} b = 1 - a \\ {(a - 2)}^{2} + {(2 - a)}^{2} = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} b = 1 - a \\ {(a - 2)}^{2} = 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} b = 1 - a \\ [\begin{matrix} a - 2 = 1 \\ a - 2 = - 1 \end{matrix} \end{matrix} \Leftrightarrow \{\begin{matrix} b = 1 - a \\ [\begin{matrix} a = 3 \\ a = 1 \end{matrix} \end{matrix} \Leftrightarrow [\begin{matrix} \{\begin{matrix} a = 3 \\ b = - 2 \end{matrix} \\ \{\begin{matrix} a = 1 \\ b = 0 \end{matrix} \end{matrix}$

Mà để N gần M hơn nên suy ra N(1; 0) Þ w = 1

Khi đó: 2z + 3w = 2(-1 + 2i) + 3

= 1 + 4i

Vậy phần ảo của số phức 2z + 3w là 4.

Câu 36:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng D đi qua M(1; 2; 3) và có vectơ chỉ phương $\vec{a} = (4; 3; - 7)$ . Phương trình tham số của D là:

A. $\{\begin{matrix} x = 4 + t \\ y = 3 + 2 t \\ z = - 7 + 3 t \end{matrix};$

B. $\{\begin{matrix} x = 1 + 4 t \\ y = 2 + 3 t \\ z = 3 - 7 t \end{matrix};$

C. $\{\begin{matrix} x = 2 + 4 t \\ y = - 3 + 3 t \\ z = 1 - 7 t \end{matrix};$

D. $\{\begin{matrix} x = 1 + t \\ y = 2 + 2 t \\ z = 1 + 3 t \end{matrix} .$

Xem đáp án

Đáp án đúng là: B

Phương trình tham số của đường thẳng D đi qua M(1; 2; 3) và có vectơ chỉ phương $\vec{a} = (4; 3; - 7)$ là:

$Δ : \{\begin{matrix} x = 1 + 4 t \\ y = 2 + 3 t \\ z = 3 - 7 t \end{matrix} .$

Câu 37:

Số phức $\frac{5 + 4 i}{3 + 6 i}$ bằng

A. $\frac{13}{15} - \frac{2}{5} i;$

B. $\frac{- 1}{15} + \frac{14}{15} i;$

C. $\frac{13}{15} + \frac{2}{5} i;$

D. $\frac{- 1}{15} - \frac{14}{15} i .$

Xem đáp án

Đáp án đúng là: A

$\frac{5 + 4 i}{3 + 6 i} = \frac{(5 + 4 i) (3 - 6 i)}{(3 + 6 i) (3 - 6 i)} = \frac{15 + 12 i - 30 i - 24 i^{2}}{3^{2} + 6^{2}}$

$= \frac{15 + 12 i - 30 i + 24}{45} = \frac{39 - 18 i}{45} = \frac{13}{15} - \frac{2}{5} i .$

Câu 38:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) đi qua A(1; 2; -3) và vuông góc với đường thẳng $d : \{\begin{matrix} x = - 10 - 2 t \\ y = 5 + t \\ z = - 3 + 3 t \end{matrix}$ có phương trình là

A. 2x - y - 3z - 2 = 0;

B. 2x - y - 3z - 9 = 0;

C. 2x + y + 3z - 7 = 0;

D. 2x + y - 3z + 9 = 0;

Xem đáp án

Đáp án đúng là: B

Véc-tơ chỉ phương của đường thẳng d là $\vec{u} = (- 2; 1; 3)$

Mặt phẳng (P) đi qua A(1; 2; -3) và vuông góc với đường thẳng d nên nhận véc-tơ $\vec{u} = (- 2; 1; 3)$ làm véc-tơ pháp tuyến

Suy ra

(P): -2(x - 1) + (y - 2) + 3(z + 3) = 0

Û -2x + 2 + y - 2 + 3z + 9 = 0

Û 2x - y - 3z - 9 = 0.

Câu 39:

Cho (H) là hình phẳng giới hạn bởi đường cong có phương trình $y = \sqrt{x}$ , nửa đường tròn $y = \sqrt{2 - x^{2}}$ với $0 \leq x \leq \sqrt{2}$ và trục hoành (phần tô đậm trong hình vẽ). Diện tích của hình (H) bằng

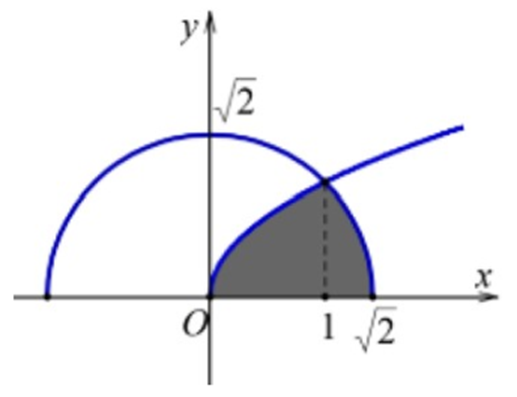
Media VietJack

A. $\frac{3 π + 1}{12};$

B. $\frac{4 π + 1}{6};$

C. $\frac{4 π + 2}{12};$

D. $\frac{3 π + 2}{12} .$

Xem đáp án

Đáp án đúng là: D

(H) là hình phẳng giới hạn bởi đường cong có phương trình $y = \sqrt{x}$ , nửa đường tròn $y = \sqrt{2 - x^{2}}$ với $0 \leq x \leq \sqrt{2}$ và trục hoành (phần tô đậm trong hình vẽ). Diện tích của hình (H) bằng

$S = \int_{0}^{1} \sqrt{x} d x + \int_{1}^{\sqrt{2}} \sqrt{2 - x^{2}} d x = \frac{2}{3} \int_{0}^{1} \frac{3}{2} \sqrt{x} d x + S_{1}$

$= {\frac{2}{3} \sqrt{x^{3}}|}_{0}^{1} + S_{1} = \frac{2}{3} + S_{1}$ (1)

+) Xét $S_{1} = \int_{1}^{\sqrt{2}} \sqrt{2 - x^{2}} d x$

Đặt $x = \sqrt{2} . \sin u$

$\Rightarrow \sqrt{2 - x^{2}} = \sqrt{2 - 2 \sin^{2} u} = \sqrt{2} . \cos u$

Và $d x = \sqrt{2} . \cos u d u$

Đổi cận

+) $x = 1 \Rightarrow u = \frac{π}{4}$

+) $x = \sqrt{2} \Rightarrow u = \frac{π}{2}$

Suy ra $S_{1} = \int_{1}^{\sqrt{2}} \sqrt{2 - x^{2}} d x = \int_{\frac{π}{4}}^{\frac{π}{2}} \sqrt{2} . \cos u . \sqrt{2} . \cos u d u$

$= \int_{\frac{π}{4}}^{\frac{π}{2}} 2 \cos^{2} u d u = \int_{\frac{π}{4}}^{\frac{π}{2}} (\cos 2 u + 1) d u = {(\frac{\sin 2 u}{2} + u)|}_{\frac{π}{4}}^{\frac{π}{2}}$

$= (0 + \frac{π}{2}) - (\frac{1}{2} + \frac{π}{4}) = - \frac{1}{2} + \frac{π}{4}$ (2)

Thay (2) vào (1) ta được

$S = \frac{2}{3} - \frac{1}{2} + \frac{π}{4} = \frac{1}{6} + \frac{π}{4} = \frac{3 π + 2}{12} .$

Câu 40:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M (1; 2; -3) và nhận làm vectơ pháp tuyến.

A. (P): 2x - y + 5z + 15 = 0;

B. (P): 2x - y + 5z - 3 = 0;

C. (P): x + y + 2z - 6 = 0;

D. (P): x + 2y - 3z + 15 = 0.

Xem đáp án

Đáp án đúng là: A

Phương trình mặt phẳng (P) đi qua điểm M (1; 2; -3) và nhận $\vec{n} = (2; - 1; 5)$ làm vectơ pháp tuyến là

(P): 2(x - 1) - (y - 2) + 5(z + 3) = 0

Û 2x - 2 - y + 2 + 5z + 15 = 0

Û 2x - y + 5z + 15 = 0.

Câu 41:

Cho hai số phức z₁ = 4 + 3i, z₂ = 5 - 7i. Số phức z₁ + z₂ bằng

A. 9 - 4i;

B. 9 - 10i;

C. 9 + 4i;

D. 9 + 10i.

Xem đáp án

Đáp án đúng là: A

Số phức z₁ + z₂ bằng

z₁ + z₂ = (4 + 3i) + (5 - 7i) = 9 - 4i.

Câu 42:

Cho hình phẳng (H) giới hạn bởi đường cong y = sin x, trục hoành và hai đường thẳng x = 0, x = p. Gọi V là thể tích khối tròn xoay tạo thành khi quay (H) xung quanh trục Ox. Mệnh đề nào dưới đây là Đúng?

A. $V = \int_{0}^{π} \sin^{2} x d x;$

B. $V = π \int_{0}^{π} \sin^{2} x d x;$

C. $V = \int_{0}^{π} \sin x d x;$

D. $V = π \int_{0}^{π} \sin x d x .$

Xem đáp án

Đáp án đúng là: B

Hình phẳng (H) giới hạn bởi đường cong y = sin x, trục hoành và hai đường thẳng x = 0, x = p. Khi đó thể tích khối tròn xoay tạo thành khi quay (H) xung quanh trục Ox là

$V = π \int_{0}^{π} \sin^{2} x d x .$

Câu 43:

Số phức z = 2 - 5i có phần ảo bằng

A. -5i;

B. -2;

C. 2;

D. -5.

Xem đáp án

Đáp án đúng là: D

Số phức z = 2 - 5i có phần ảo bằng -5.

Câu 44:

Cho $\int_{0}^{2} f (x) d x = 7$ và $\int_{0}^{2} g (x) d x = 3$ . Khi đó $\int_{0}^{2} [f (x) + g (x)] d x$ bằng

A. 9;

B. 21;

C. 10;

D. 4.

Xem đáp án

Đáp án đúng là: C

$\int_{0}^{2} [f (x) + g (x)] d x = \int_{0}^{2} f (x) d x + \int_{0}^{2} g (x) d x$

= 7 + 3 = 10.

Câu 45:

Gọi z₁, z₂ là hai nghiệm phức của phương trình z² + 2z + 10 = 0. Giá trị của biểu thức |z₁| + |z₂| bằng

A. $4 \sqrt{10};$

B. $\sqrt{10};$

C. $3 \sqrt{10};$

D. $2 \sqrt{10} .$

Xem đáp án

Đáp án đúng là: D

z₁, z₂ là hai nghiệm phức của phương trình z² + 2z + 10 = 0

Nên theo Vi-ét ta có z₁z₂ = 10

Þ |z₁z₂| = |z₁|.|z₂| = 10

$\Rightarrow |z_{1}| = |z_{2}| = \sqrt{10}$

Khi đó giá trị của biểu thức |z₁| + |z₂| bằng

$|z_{1}| + |z_{2}| = \sqrt{10} + \sqrt{10} = 2 \sqrt{10} .$

Câu 46:

Cho hàm số f (x) có đạo hàm liên tục trên ℝ, f (0) = 0, f '(0) ¹ 0 và thỏa mãn hệ thức f (x).f '(x) + 18x² = (3x² + x).f '(x) + (6x + 1).f (x), "x Î ℝ.

Biết $\int_{2}^{3} [2 f (x) + 2] \ln x d x = a + b \ln 2 + c \ln 3$ , với a, b, c là các số nguyên. Tính giá trị biểu thức P = 2a + 3b + c.

A. P = 18;

B. P =15;

C. P = -32;

D. P = -26.

Xem đáp án

Đáp án đúng là: D

Ta có:

f (x).f '(x) + 18x² = (3x² + x).f '(x) + (6x + 1).f '(x) (1)

+) Xét phương trình f '(x) = 0

Khi đó phương trình (1) trở thành 18x² = 0 Û x = 0

Mà f '(0) ¹ 0 nên suy ra f '(x) ¹ 0 với mọi x

+) Với x = 0 thay vào (1) ta có

f '(0) = 0 (vô lí nên suy ra x = 0 không là nghiệm của phương trình)

Lấy nguyên hàm hai vế của phương trình (1) nên suy ra

$(1) \Leftrightarrow \int [f (x) . f' (x) + 18 x^{2}] d x = \int [(3 x^{2} + x) f' (x) + (6 x + 1) f (x)] d x$

$\Leftrightarrow \int [f (x) . f' (x) + 18 x^{2}] d x = \int [(3 x^{2} + x) f' (x) + {(3 x^{2} + x)}^{'} f (x)] d x$

$\Leftrightarrow \frac{1}{2} f^{2} (x) + 6 x^{3} = (3 x^{2} + x) f (x) + C$ (2)

Mà f (0) = 0 nên thay x = 0 vào (2) ta thấy

(2) Û C = 0

Vậy suy ra $\frac{1}{2} f^{2} (x) + 6 x^{3} = (3 x^{2} + x) f (x)$

$\Leftrightarrow f^{2} (x) - 2 (3 x^{2} + x) f (x) + 12 x^{3} = 0$

$\Leftrightarrow f^{2} (x) - 6 x^{2} . f (x) - 2 x f (x) + 12 x^{3} = 0$

$\Leftrightarrow f (x) [f (x) - 6 x^{2}] - 2 x [f (x) - 6 x^{2}] = 0$

$\Leftrightarrow [f (x) - 2 x] [f (x) - 6 x^{2}] = 0$ $\Rightarrow [\begin{matrix} f (x) = 2 x \\ f (x) = 6 x^{2} \end{matrix} \Rightarrow [\begin{matrix} f' (x) = 2 \\ f' (x) = 12 x \end{matrix}$

Mà do f '(0) ¹ 0 nên suy ra ta chọn f (x) = 2x

Khi đó

$\int_{2}^{3} [2 f (x) + 2] \ln x d x = \int_{2}^{3} (4 x + 2) \ln x d x$

Đặt $\{\begin{matrix} u = \ln x \Rightarrow d u = \frac{1}{x} d x \\ d v = (4 x + 2) d x \Rightarrow v = 2 x^{2} + 2 x \end{matrix}$

Nên suy ra $\int_{2}^{3} (4 x + 2) \ln x d x$

$= {(2 x^{2} + 2 x) \ln x|}_{2}^{3} - \int_{2}^{3} (2 x + 2) d x$

$= {(2 x^{2} + 2 x) \ln x|}_{2}^{3} - {(x^{2} + 2 x)|}_{2}^{3}$

= 24ln 3 - 12ln 2 - 15 + 8

= -7 - 12ln 2 + 24ln 3.

Mà ta biết $\int_{2}^{3} [2 f (x) + 2] \ln x d x = a + b \ln 2 + c \ln 3$

Nên suy ra được a = -7, b = -12, c = 24

Khi đó: P = 2a + 3b + c

= 2.(-7) + 3.(-12) + 24 = -26.

Câu 47:

Tính tích phân

I = \int_{1}^{2} \frac{1}{x^{2}} d x

A. $I = \frac{5}{4};$

B. $I = \frac{1}{2};$

C. $I = \frac{- 5}{6};$

D. $I = \frac{2}{3} .$

Xem đáp án

Đáp án đúng là: B

$I = \int_{1}^{2} \frac{1}{x^{2}} d x = - \int_{1}^{2} \frac{- 1}{x^{2}} d x = {- \frac{1}{x}|}_{1}^{2} = \frac{- 1}{2} + 1 = \frac{1}{2} .$

Câu 48:

Tìm họ nguyên hàm của hàm số

f (x) = \frac{1}{x}

A. $F (x) = - \frac{1}{x^{2}} + C;$

B. $F (x) = \frac{1}{2} \ln |x| + C;$

C. F (x) = ln |x| + C;

D. F (x) = -x² + C.

Xem đáp án

Đáp án đúng là: C

$f (x) = \frac{1}{x} \Rightarrow F (x) = \int f (x) d x = \int \frac{1}{x} d x$

= ln |x| + C.

Câu 49:

Cho số phức z = 4 + 3i, khi đó số phức liên hợp $\bar{z}$ của z là

A. $\bar{z} = 3 + 4 i;$

B. $\bar{z} = - 4 + 3 i;$

C. $\bar{z} = 4 - 3 i;$

D. $\bar{z} = - 3 + 4 i .$

Xem đáp án

Đáp án đúng là: C

Với z = 4 + 3i, khi đó số phức liên hợp $\bar{z}$ của z là $\bar{z} = 4 - 3 i .$

Câu 50:

Diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = f (x), y = g (x) liên tục trên [a; b] và hai đường thẳng x = a, x = b (a < b) được tính theo công thức

A. $S = \int_{a}^{b} |f^{2} (x) + g^{2} (x)| d x;$

B. $S = π \int_{a}^{b} |f (x) - g (x)| d x;$

C. $S = \int_{a}^{b} |f (x) + g (x)| d x;$

D. $S = \int_{a}^{b} |f (x) - g (x)| d x .$

Xem đáp án

Đáp án đúng là: D

Diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = f (x), y = g (x) liên tục trên [a; b] và hai đường thẳng x = a, x = b (a < b) được tính theo công thức $S = \int_{a}^{b} |f (x) - g (x)| d x .$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 11

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương